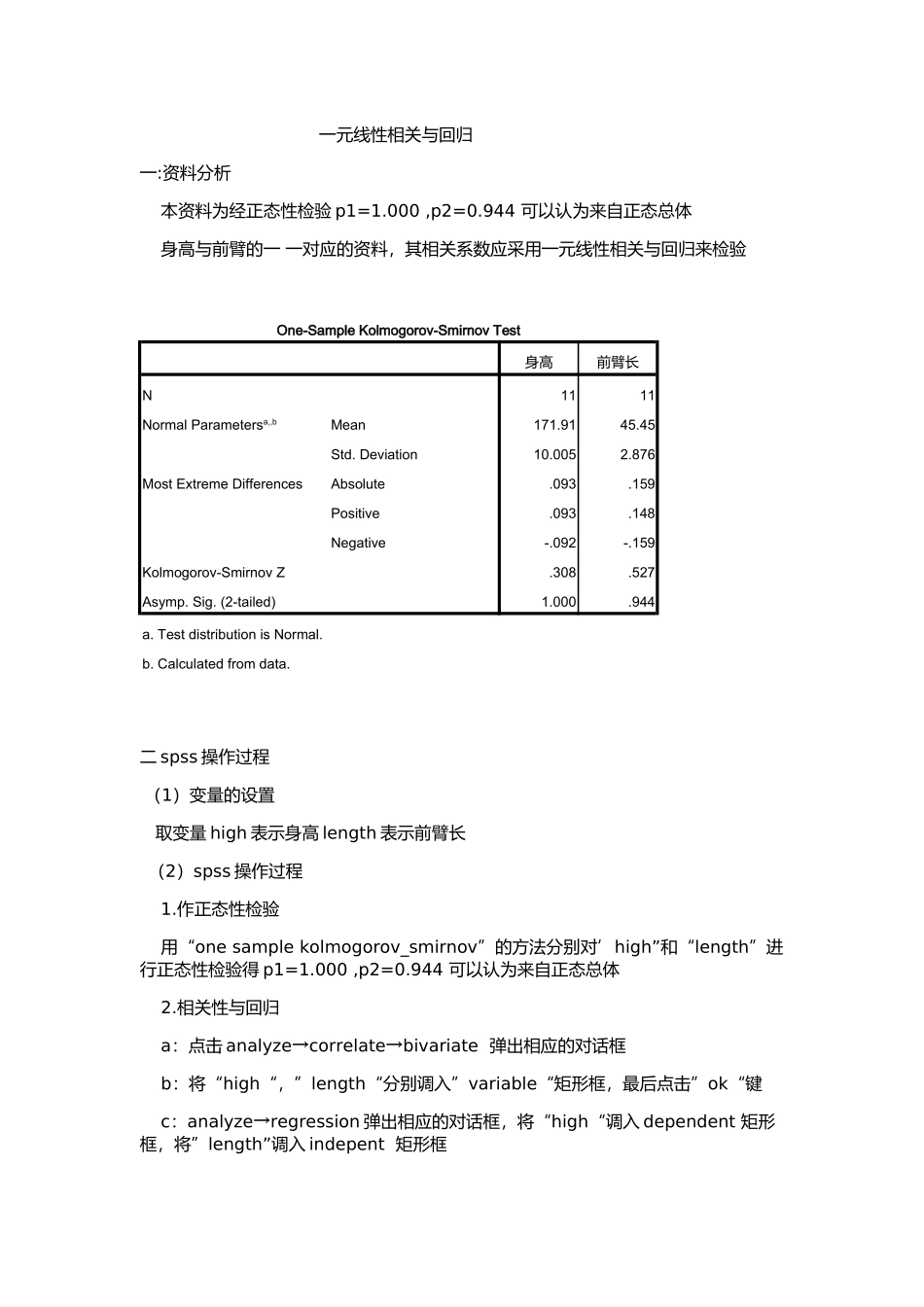
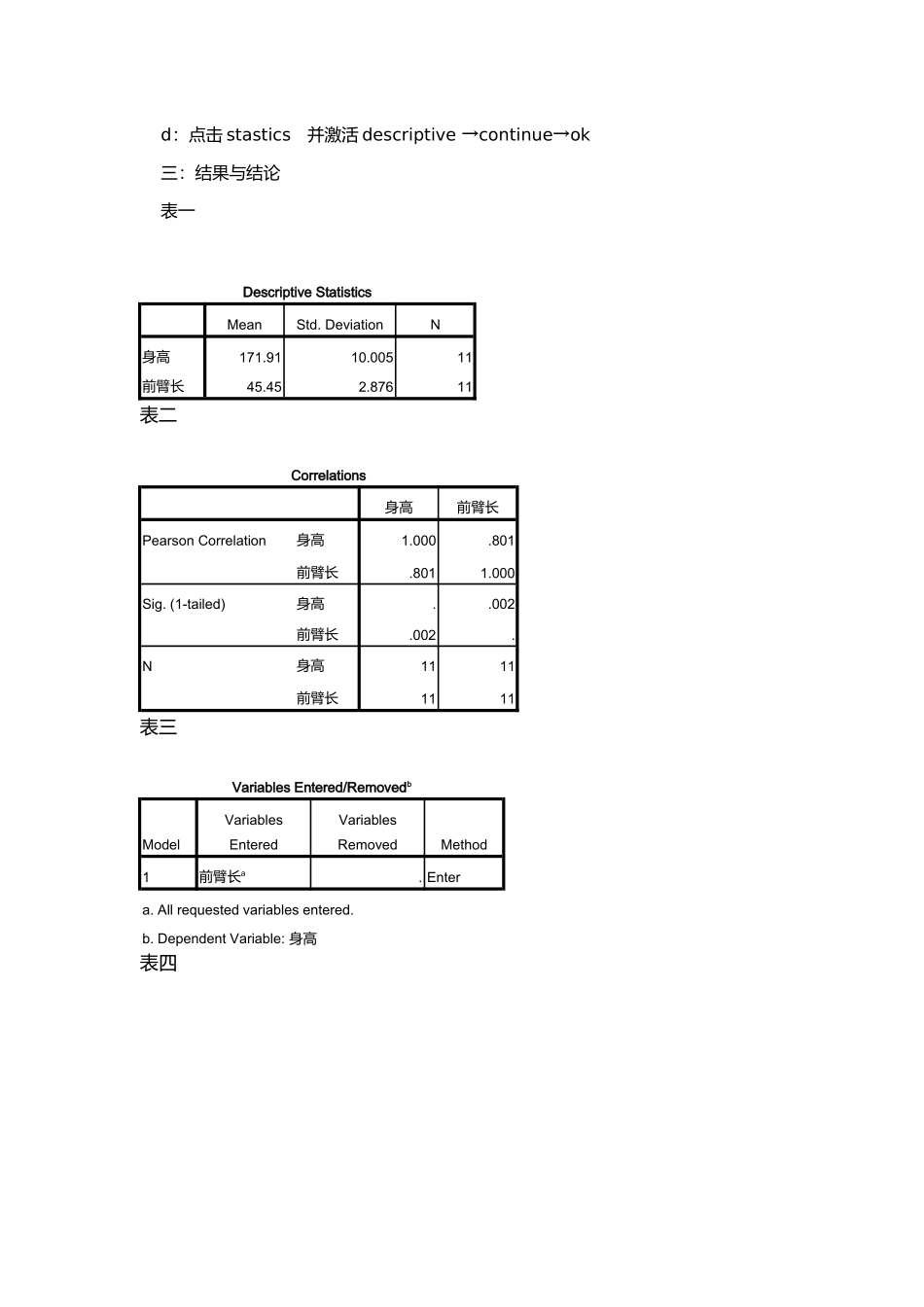
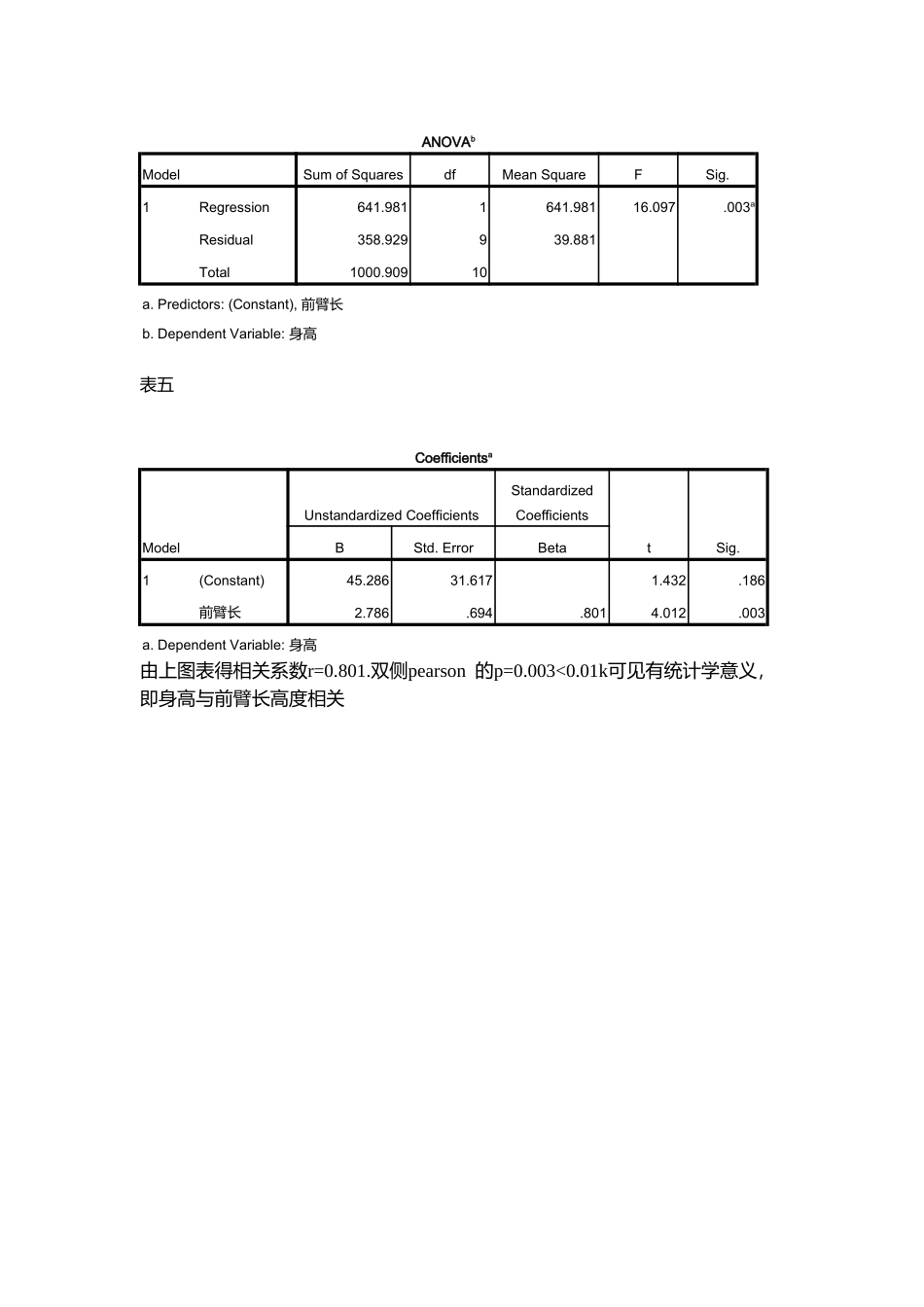
一元线性相关与回归一:资料分析本资料为经正态性检验p1=1.000,p2=0.944可以认为来自正态总体身高与前臂的一一对应的资料,其相关系数应采用一元线性相关与回归来检验One-SampleKolmogorov-SmirnovTest身高前臂长N1111NormalParametersa,,bMean171.9145.45Std.Deviation10.0052.876MostExtremeDifferencesAbsolute.093.159Positive.093.148Negative-.092-.159Kolmogorov-SmirnovZ.308.527Asymp.Sig.(2-tailed)1.000.944a.TestdistributionisNormal.b.Calculatedfromdata.二spss操作过程(1)变量的设置取变量high表示身高length表示前臂长(2)spss操作过程1.作正态性检验用“onesamplekolmogorov_smirnov”的方法分别对’high”和“length”进行正态性检验得p1=1.000,p2=0.944可以认为来自正态总体2.相关性与回归a:点击analyze→correlate→bivariate弹出相应的对话框b:将“high“,”length“分别调入”variable“矩形框,最后点击”ok“键c:analyze→regression弹出相应的对话框,将“high“调入dependent矩形框,将”length”调入indepent矩形框d:点击stastics并激活descriptive→continue→ok三:结果与结论表一DescriptiveStatisticsMeanStd.DeviationN身高171.9110.00511前臂长45.452.87611表二Correlations身高前臂长PearsonCorrelation身高1.000.801前臂长.8011.000Sig.(1-tailed)身高..002前臂长.002.N身高1111前臂长1111表三VariablesEntered/RemovedbModelVariablesEnteredVariablesRemovedMethod1前臂长a.Entera.Allrequestedvariablesentered.b.DependentVariable:身高表四ANOVAbModelSumofSquaresdfMeanSquareFSig.1Regression641.9811641.98116.097.003aResidual358.929939.881Total1000.90910a.Predictors:(Constant),前臂长b.DependentVariable:身高表五CoefficientsaModelUnstandardizedCoefficientsStandardizedCoefficientstSig.BStd.ErrorBeta1(Constant)45.28631.6171.432.186前臂长2.786.694.8014.012.003a.DependentVariable:身高由上图表得相关系数r=0.801.双侧pearson的p=0.003<0.01k可见有统计学意义,即身高与前臂长高度相关