截面几何性质

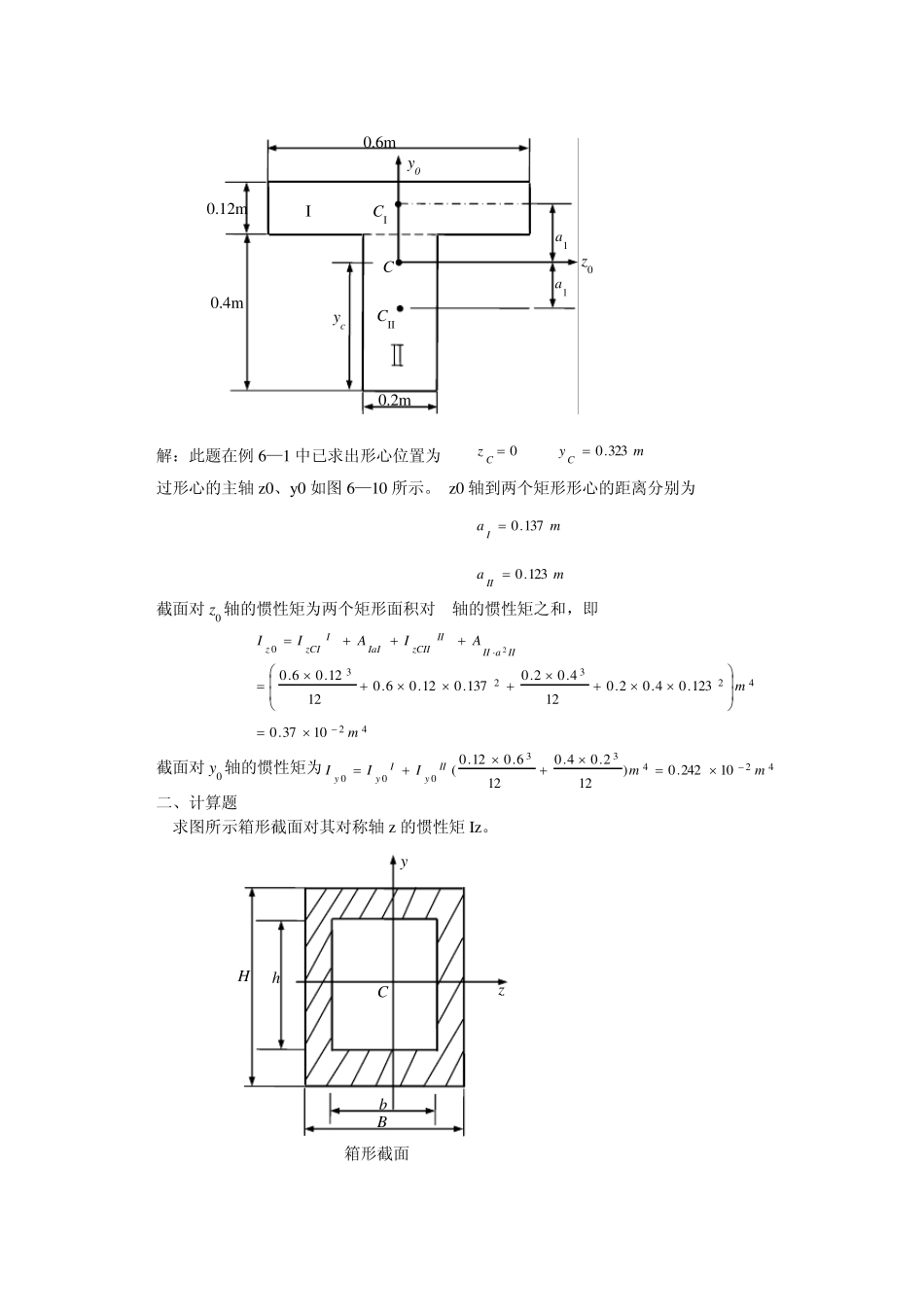
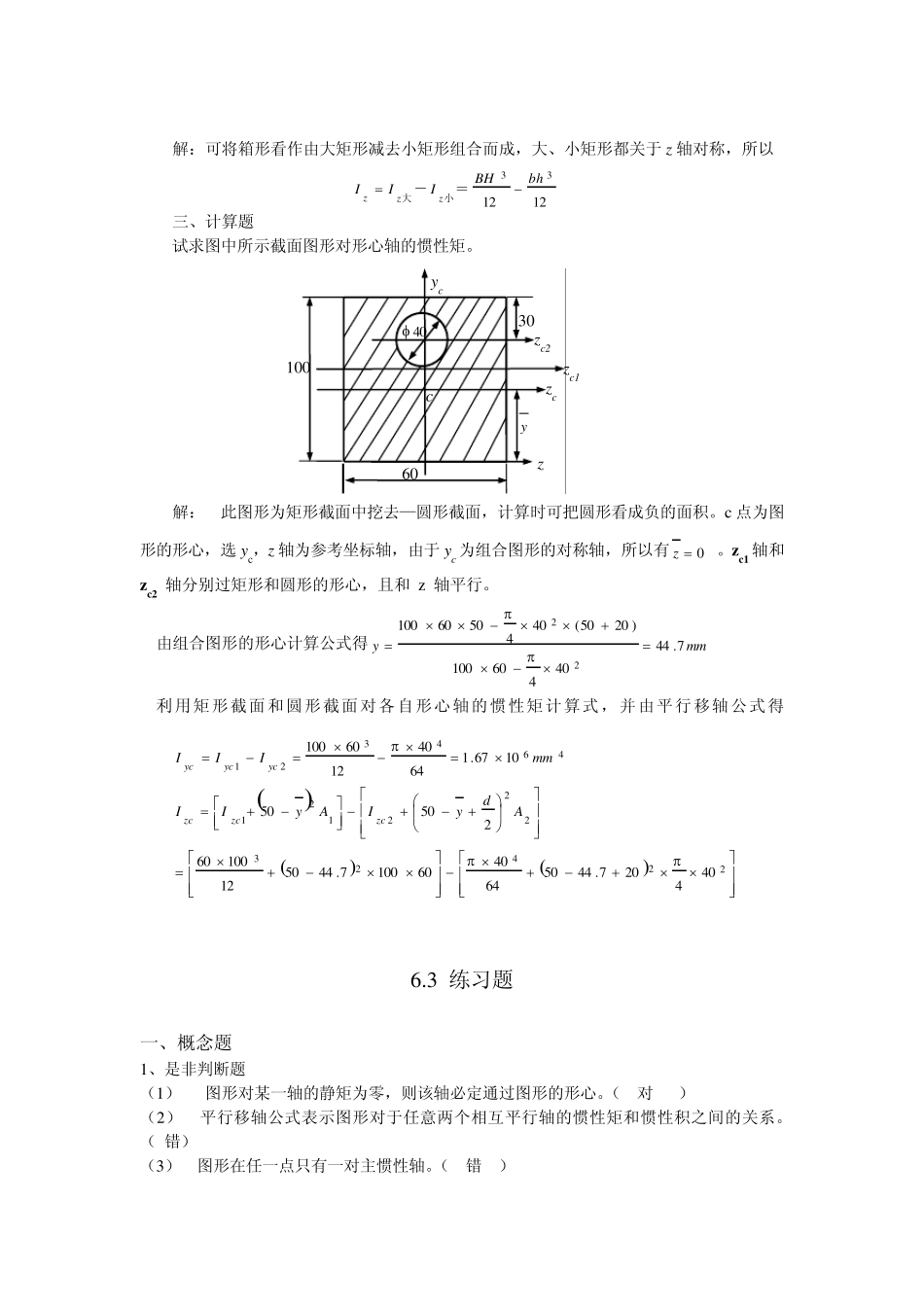
第六章 截面几何性质 6.1 预备知识 一、基本概念 1、 组合截面惯性矩的计算 工程中常遇到组合截面，这些组合截面有的是由几个简单图形组成（图a、b、c），有的是由几个型钢截面组成（图d）。在计算组合截面对某轴的惯性矩时，根据惯性矩的定义，可分别计算各组成部分对该轴的惯性矩，然后再相加。 在计算组合截面的形心主惯性矩时，应首先确定形心的位置，然后过形心选择一对便于计算惯性矩和惯性积的坐标轴并算出组合截面对这对轴的惯性矩和惯性积，通过式（6—16）、（6—17）便可确定形心主轴的位置和算出截面对形心主轴的惯性矩。 二、重点与难点 1、 2、 3、 三、解题方法要点 6.2 典型题解 一、计算题 求图中截面的形心主惯性矩。 (b) (c) (d) (a) 解：此题在例6—1 中已求出形心位置为 0Cz my C323.0 过形心的主轴 z0、y0 如图 6—10 所示。 z0 轴到两个矩形形心的距离分别为 ma I137.0 ma II123.0 截面对 z0 轴的惯性矩为两个矩形面积对 轴的惯性矩之和，即 424232301037.0123.04.02.0124.02.0137.012.06.01212.06.02mmAIAIIIIaIIIIzCIIIaIIzCIz 截面对 y0 轴的惯性矩为4243300010242.0)122.04.0126.012.0(mmIIIIIyIyy 二、计算题 求图所示箱形截面对其对称轴 z 的惯性矩 Iz。 0.2m 0.4m 0.12m 0.6m yc C CI CII 1a 1aI y0 z0 B b H h C y z 箱形截面 解：可将箱形看作由大矩形减去小矩形组合而成，大、小矩形都关于z 轴对称，所以 121233bhBHIIIzzz＝－小大 三、计算题 试求图中所示截面图形对形心轴的惯性矩。 解： 此图形为矩形截面中挖去—圆形截面，计算时可把圆形看成负的面积。c 点为图形的形心，选 yc，z 轴为参考坐标轴，由于yc 为组合图形的对称轴，所以有0z 。zc1 轴和zc2 轴分别过矩形和圆形的形心，且和 z 轴平行。 由组合图形的形心计算公式得mmy7.4440460100)2050(404506010022 利用矩形截面和圆形截面对各自形心轴的惯性矩计算式，并由平行移轴公式得22423222121464321404207.44506440601007.44501210060250501067.164401260100AdyIAyIImmIIIzczczcycycyc...