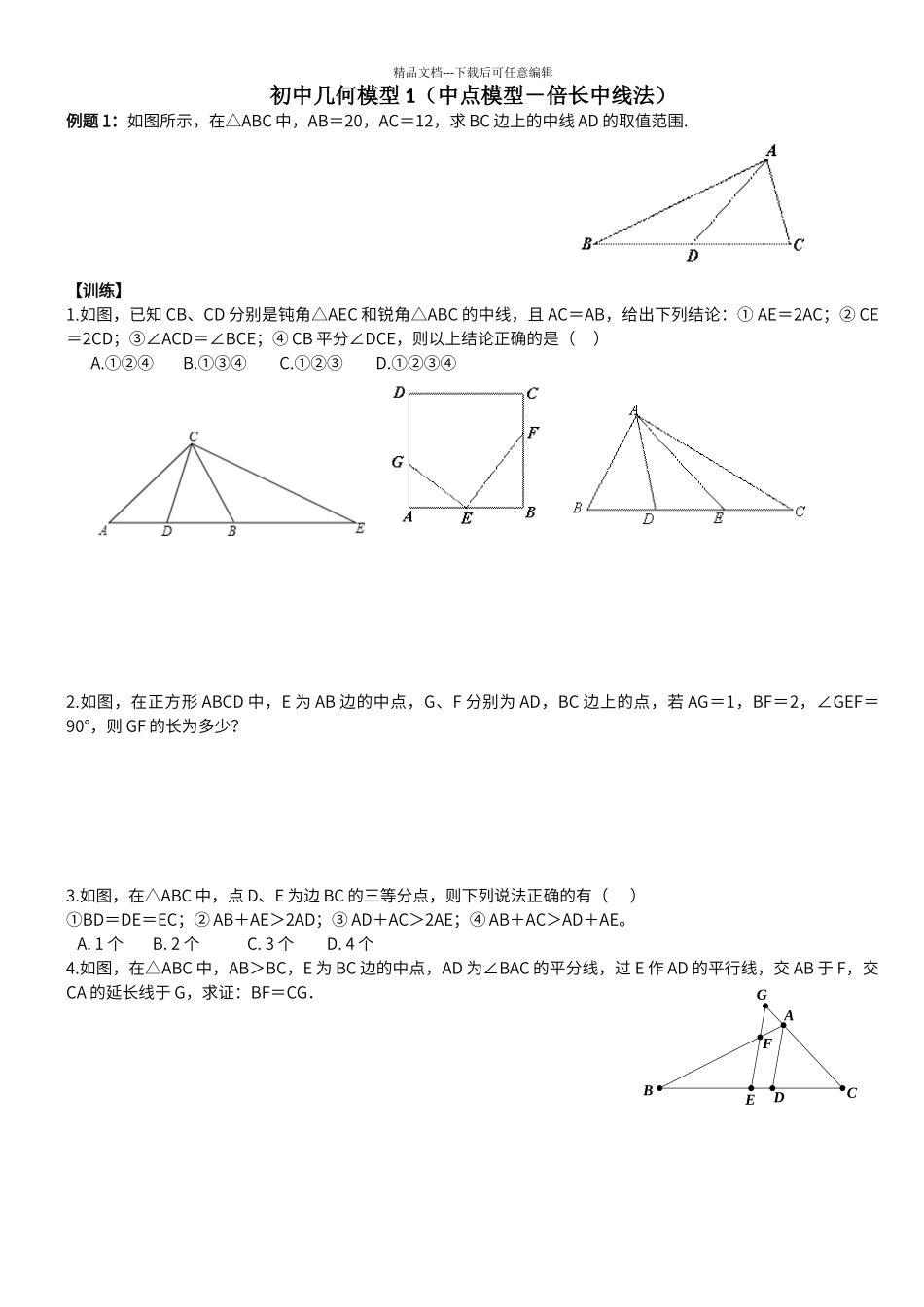
精品文档---下载后可任意编辑初中几何模型 1(中点模型-倍长中线法)例题 1:如图所示,在△ABC 中,AB=20,AC=12,求 BC 边上的中线 AD 的取值范围.【训练】1.如图,已知 CB、CD 分别是钝角△AEC 和锐角△ABC 的中线,且 AC=AB,给出下列结论:① AE=2AC;② CE=2CD;③∠ACD=∠BCE;④ CB 平分∠DCE,则以上结论正确的是( )A.①②④ B.①③④ C.①②③ D.①②③④ 2.如图,在正方形 ABCD 中,E 为 AB 边的中点,G、F 分别为 AD,BC 边上的点,若 AG=1,BF=2,∠GEF=90°,则 GF 的长为多少?3.如图,在△ABC 中,点 D、E 为边 BC 的三等分点,则下列说法正确的有( )①BD=DE=EC;② AB+AE>2AD;③ AD+AC>2AE;④ AB+AC>AD+AE。 A. 1 个 B. 2 个 C. 3 个 D. 4 个4.如图,在△ABC 中,AB>BC,E 为 BC 边的中点,AD 为∠BAC 的平分线,过 E 作 AD 的平行线,交 AB 于 F,交CA 的延长线于 G,求证:BF=CG.FGEDBCA精品文档---下载后可任意编辑5.如图所示,已知在△ABC 中,AD 是 BC 边上的中线,F 是 AD 上的一点,连接 BE 并延长交 AC 于点 F,AE=EF,求证:AC=BF.6.如图所示,在△ABC 中,分别以 AB、AC 为直角边向外做等腰直角三角形△ABD 和△ACE,F 为 BC 边上中点,FA 的延长线交 DE 于点 G,求证:① DE=2AF;② FG⊥DE.7.如图所示,在 Rt△ABC 中,∠BAC=90°,点 D 为 BC 的中点,点 E、F 分别为 AB、AC 上的点,且 ED⊥FD.以线段 BE、EF、FC 为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形,或者是钝角三角形?8.四边形 ABCD 是矩形,E 是 BC 边上的中点,△ABE 沿着直线 AE 翻折,点 B 落在点 F 处,直线 AF 与直线 CD 交于点 G,请探究线段 AB、AG、GC 之间的关系.(选做)9.如图所示,△ABC 中,点 D 是 BC 的中点,且∠BAD=∠DAE,过点 C 作 CF//AB,交 AE 的延长线于点 F,求证:AF+CF=AB.FDBCAEGFBCADEFDABCEFDBCAE精品文档---下载后可任意编辑