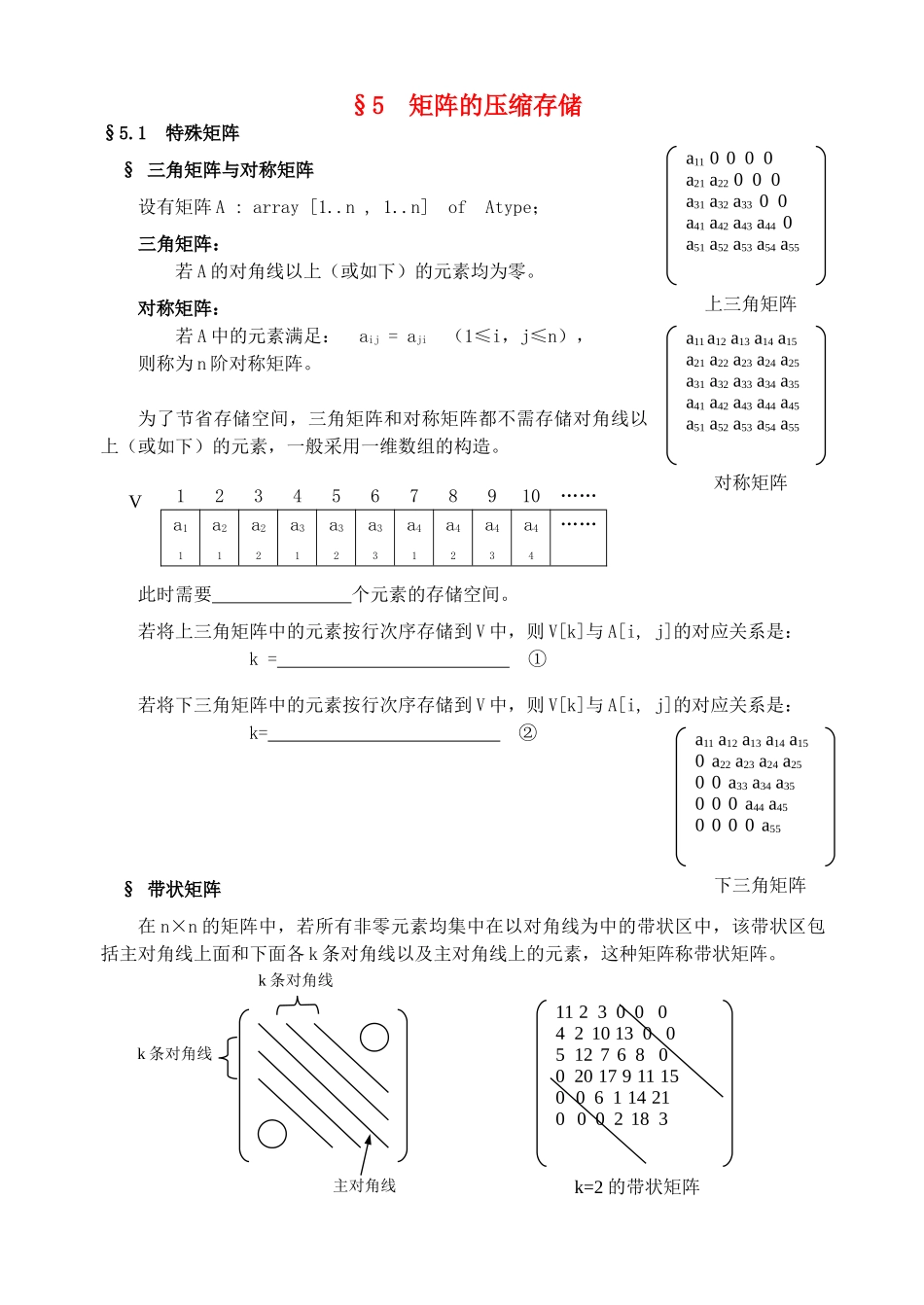
§5 矩阵的压缩存储§5.1 特殊矩阵§ 三角矩阵与对称矩阵设有矩阵 A : array [1..n , 1..n] of Atype;三角矩阵:若 A 的对角线以上(或如下)的元素均为零。 对称矩阵:若 A 中的元素满足: aij = aji (1≤i,j≤n),则称为 n 阶对称矩阵。为了节省存储空间,三角矩阵和对称矩阵都不需存储对角线以上(或如下)的元素,一般采用一维数组的构造。12345678910……a11a21a22a31a32a33a41a42a43a44……此时需要 个元素的存储空间。若将上三角矩阵中的元素按行次序存储到 V 中,则 V[k]与 A[i, j]的对应关系是: k = ①若将下三角矩阵中的元素按行次序存储到 V 中,则 V[k]与 A[i, j]的对应关系是: k= ②§ 带状矩阵在 n×n 的矩阵中,若所有非零元素均集中在以对角线为中的带状区中,该带状区包括主对角线上面和下面各 k 条对角线以及主对角线上的元素,这种矩阵称带状矩阵。a11 0 0 0 0a21 a22 0 0 0a31 a32 a33 0 0a41 a42 a43 a44 0a51 a52 a53 a54 a55上三角矩阵a11 a12 a13 a14 a15a21 a22 a23 a24 a25a31 a32 a33 a34 a35a41 a42 a43 a44 a45a51 a52 a53 a54 a55对称矩阵V:a11 a12 a13 a14 a150 a22 a23 a24 a250 0 a33 a34 a350 0 0 a44 a450 0 0 0 a55下三角矩阵11 2 3 0 0 04 2 10 13 0 05 12 7 6 8 00 20 17 9 11 150 0 6 1 14 210 0 0 2 18 3k=2 的带状矩阵主对角线k 条对角线k 条对角线在带状矩阵 A 中,i – j > k 或 ③ 时,A[ i , j ] = 0 。对于带状区以外的 0 元素可不必存储,而只存储带状区中的元素。带状区中有 ④ 个元素,但为了以便起见,每行当作 2k+1 个元素来存储,此时存储的元素个数为 (2k+1)×n 个。【参照答案】:① i×(i-1) / 2 + j② (n+(n-i+1))×(i-1) + (j-i+1)③ j - i > k④ n×n – (n-k)×(n–k–1)§5.2 稀疏矩阵 大多数元素的值为零的矩阵称为稀疏矩阵,为了节省存储空间,可以采用三元组或十字链表等措施来存储。 § 三元组表达法三元组表达法是用三元组(i , j , v)表达矩阵的每个非零元素。第一行的 i , j , v 分别表达矩阵 A 的行数、列数、非零元素个数,第二行开始的 i , j , v 分别表达矩阵 A 中每个非零元素的行下标、列下标、元素的值。 【例 5.2_1】 §三元组矩阵转置对矩...