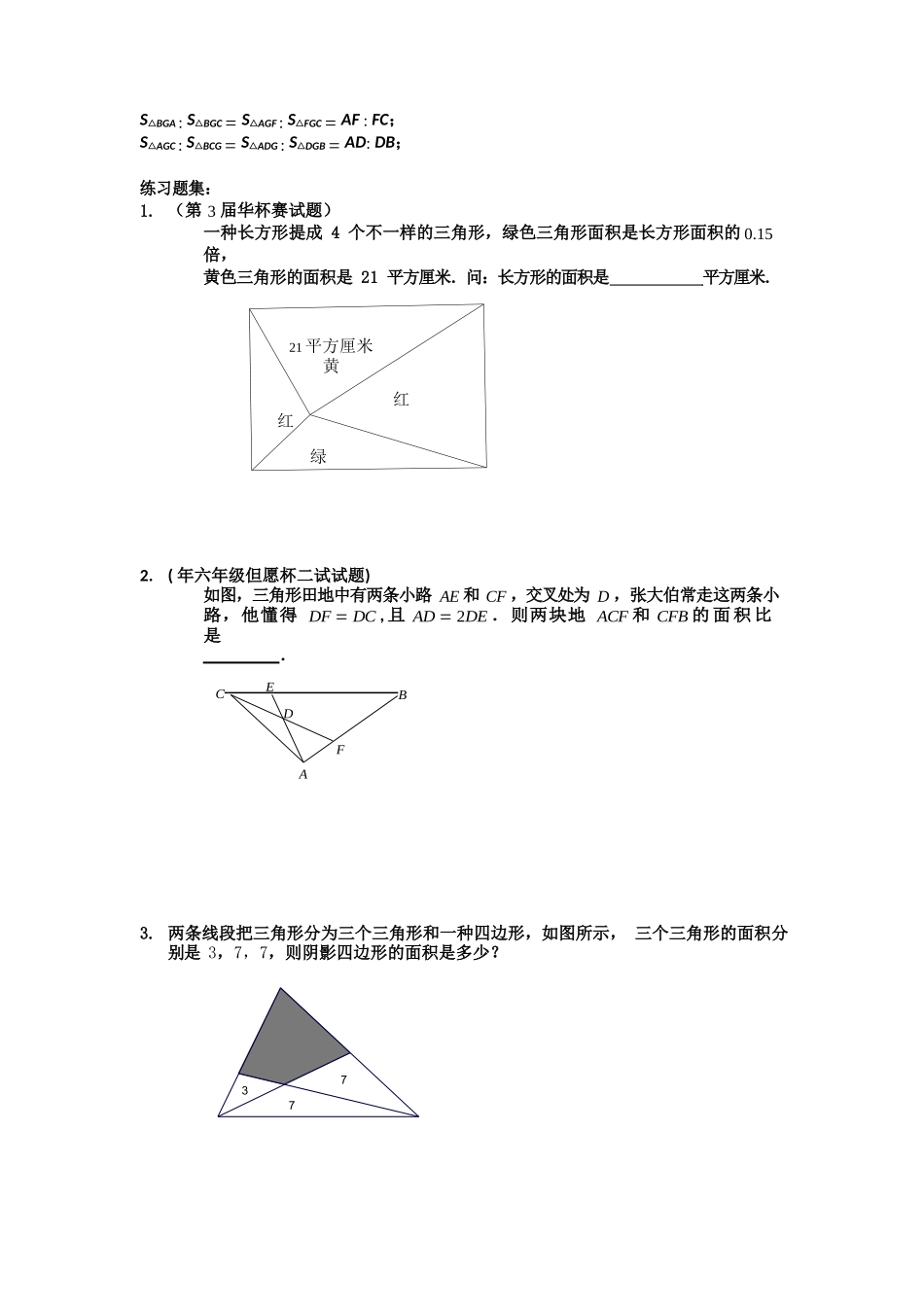
S1S2AEDEAS 2S 1OS 4S 3● 小升初复习专题 平面几何(直线模型)一、等积变换模型① 等底等高的两个三角形面积相等; ② 两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; ABabCD 如左图 S1 : S2 a : b ③ 夹在一组平行线之间的等积变形,如右上图 S△ACD S△BCD ; 反之,假如 S△ACD S△BCD ,则可知直线 AB 平行于 CD . ④ 正方形的面积等于对角线长度平方的二分之一;⑤ 三角形面积等于与它等底等高的平行四边形面积的二分之一; 二、鸟头定理(共角定理)模型两个三角形中有一种角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 如图在△ABC 中,D, E 分别是 AB, AC 上的点如图 ⑴(或 D 在 BA 的延长线上,E 在 AC上),则 S△ABC : S△ADE (AB AC) : (AD AE) DABCBC图 ⑴ 图 ⑵ 推理过程连接 BE ,再运用等积变换模型即可 三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”): DBC2DFEADGF① S1 : S2 S4 : S3 或者 S1 S3 S2 S4 ② AO : OC S1 S2 : S4 S3 蝴蝶定理为我们提供了处理不规则四边形的面积问题的一种途径.通过构造模型,首先可以使不规则四边形的面积关系与四边形内的三角形相联络;另首先,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝴蝶定理”): AaD S 1S 2 O S 4S 3BbC① S : S a2 : b2 13② S : S : S : S a2 : b2 : ab : ab ; 1324③ 梯形 S 的对应份数为a b2 .四、相似模型相似三角形性质: A BGEFDC(金字塔模型) BGC (沙漏模型) ① AD AE DE AF ; ABACBCAG② S△ADE:S△ABC AF : AG . 所谓的相似三角形,就是形状相似,大小不一样的三角形(只要其形状不变化,不管大小怎样变化它们都相似),与相似三角形有关的常用的性质及定理如下: ⑴ 相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵ 相似三角形的面积比等于它们相似比的平方; 五、燕尾定理模型AS△ABG : S△AGC S△BGE : S△EGC BE : EC; BEC21 平方厘米黄红红绿737S△BGA : S△BGC S△AGF : S△FGC A...