机械原理课后习题答案(朱理)

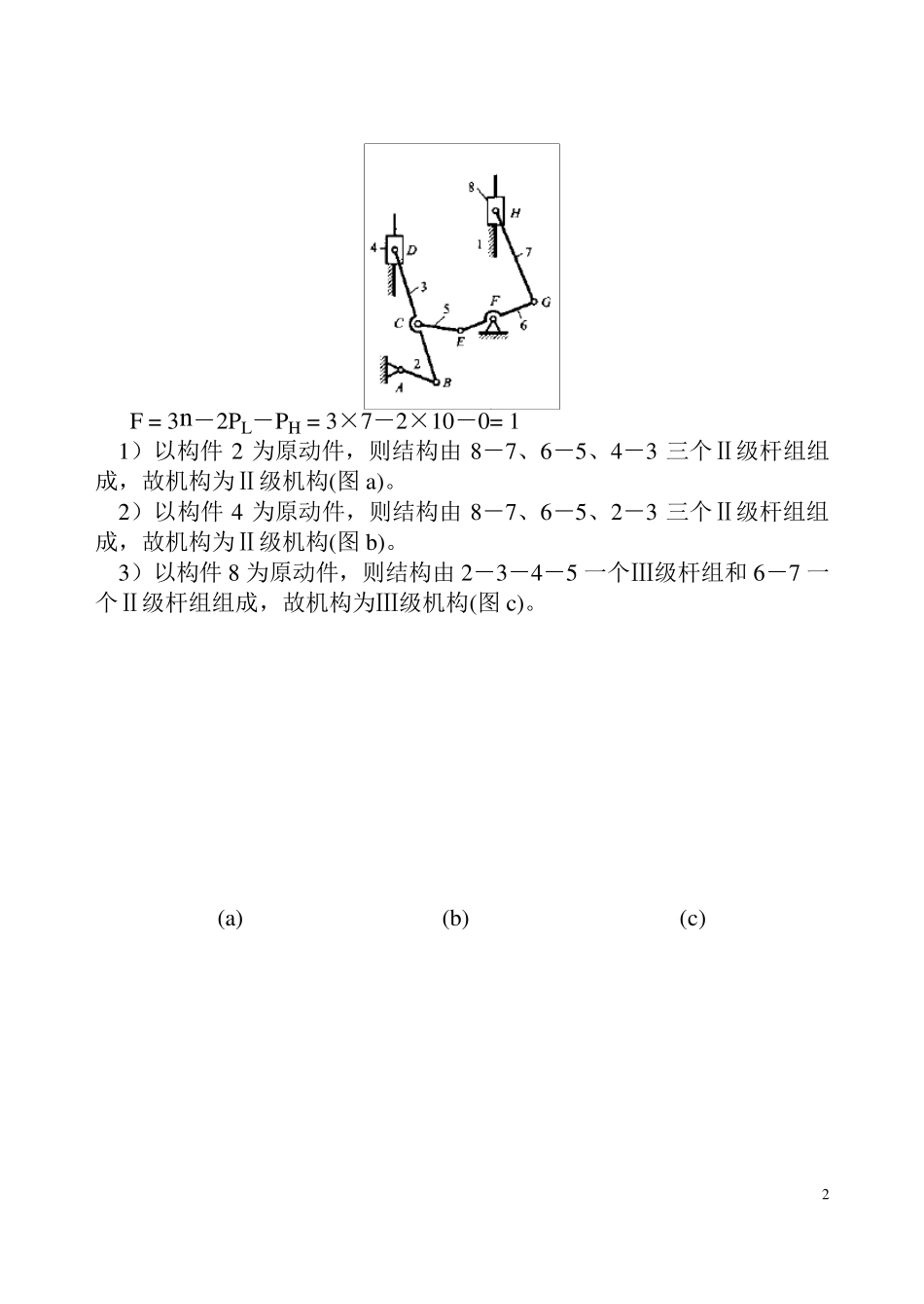
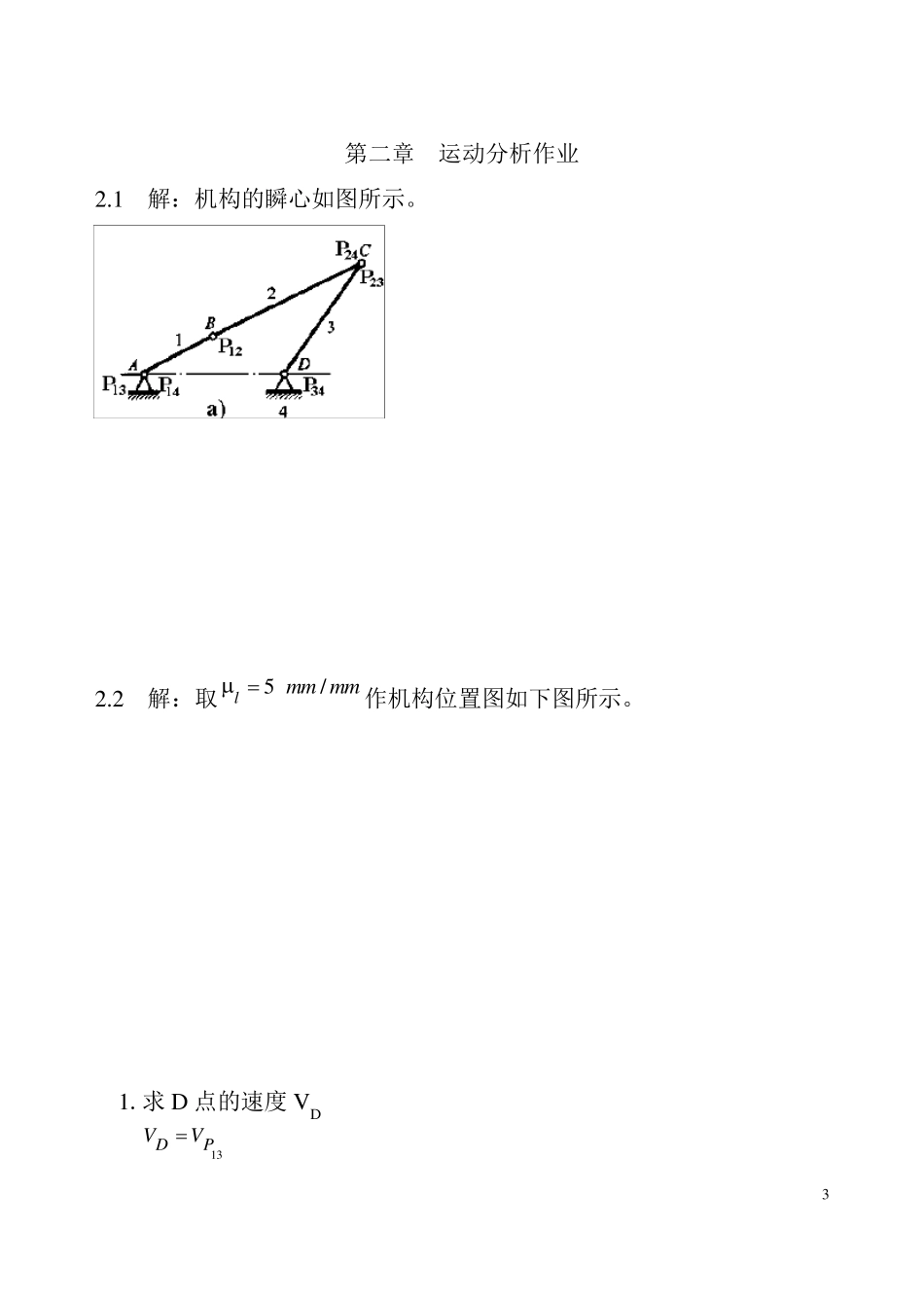
1 机 械 原 理 部 分 课 后 答 案 第一章 结构分析作业 1.2 解： F = 3n－2PL－PH = 3×3－2×4－1= 0 该机构不能运动，修改方案如下图： 1.2 解： （a）F = 3n－2PL－PH = 3×4－2×5－1= 1 A 点为复合铰链。 （b）F = 3n－2PL－PH = 3×5－2×6－2= 1 B、E 两点为局部自由度, F、C 两点各有一处为虚约束。 （c）F = 3n－2PL－PH = 3×5－2×7－0= 1 FIJKLM 为虚约束。 1.3 解： 2 F = 3n－2PL－PH = 3×7－2×10－0= 1 1）以构件 2 为原动件，则结构由 8－7、6－5、4－3 三个Ⅱ级杆组组成，故机构为Ⅱ级机构(图 a)。 2）以构件 4 为原动件，则结构由 8－7、6－5、2－3 三个Ⅱ级杆组组成，故机构为Ⅱ级机构(图 b)。 3）以构件 8 为原动件，则结构由 2－3－4－5 一个Ⅲ级杆组和 6－7 一个Ⅱ级杆组组成，故机构为Ⅲ级机构(图 c)。 (a) (b) (c) 3 第二章 运动分析作业 2.1 解：机构的瞬心如图所示。 2.2 解：取m mm ml/5作机构位置图如下图所示。 1.求 D 点的速度 V D 13PDVV 4 而 25241314PPAEVVED ，所以 smmVVED/14425241502524 2. 求ω1 sradlVAEE/25.11201501 3. 求ω2 因 98382412141212PPPP ，所以srad /46.0983825.1983812  4. 求C 点的速度VC smmCPVlC/2.10154446.0242 2.3 解：取mmmml/1作机构位置图如下图a 所示。 1. 求B2 点的速度VB2 VB2 =ω1×LAB =10×30= 300 mm/s 2.求B3 点的速度VB3 VB3 ＝ VB2 ＋ VB3B2 大小 ？ ω1×LAB ？ 方向 ⊥BC ⊥AB ∥BC 取mmsmmv/10作速度多边形如下图b 所示，由图量得： mmpb223  ，所以 smmpbVvB/270102733 由图a 量得：BC=123 mm , 则 mmBCllBC1231123 5 3. 求D 点和E 点的速度V D 、V E 利用速度影像在速度多边形，过p 点作⊥CE，过b3 点作⊥BE，得到 e点；过e 点作⊥pb3，得到 d 点 , 由图量得：mmpd15， mmpe17， 所以 smmpdVvD/1501015 ， smmpeVvE/1701017； smmbbVvBB/17010173223 4. 求ω3 sradlVBCB/2.212327033 5. 求nBa 2 22212/30003010smmlaABnB 6 6. 求3Ba aB3 ＝ aB3n ＋ aB3t ＝ aB2 ＋ aB3B2k ＋ aB3B...