材料力学第七章习题选及其解答

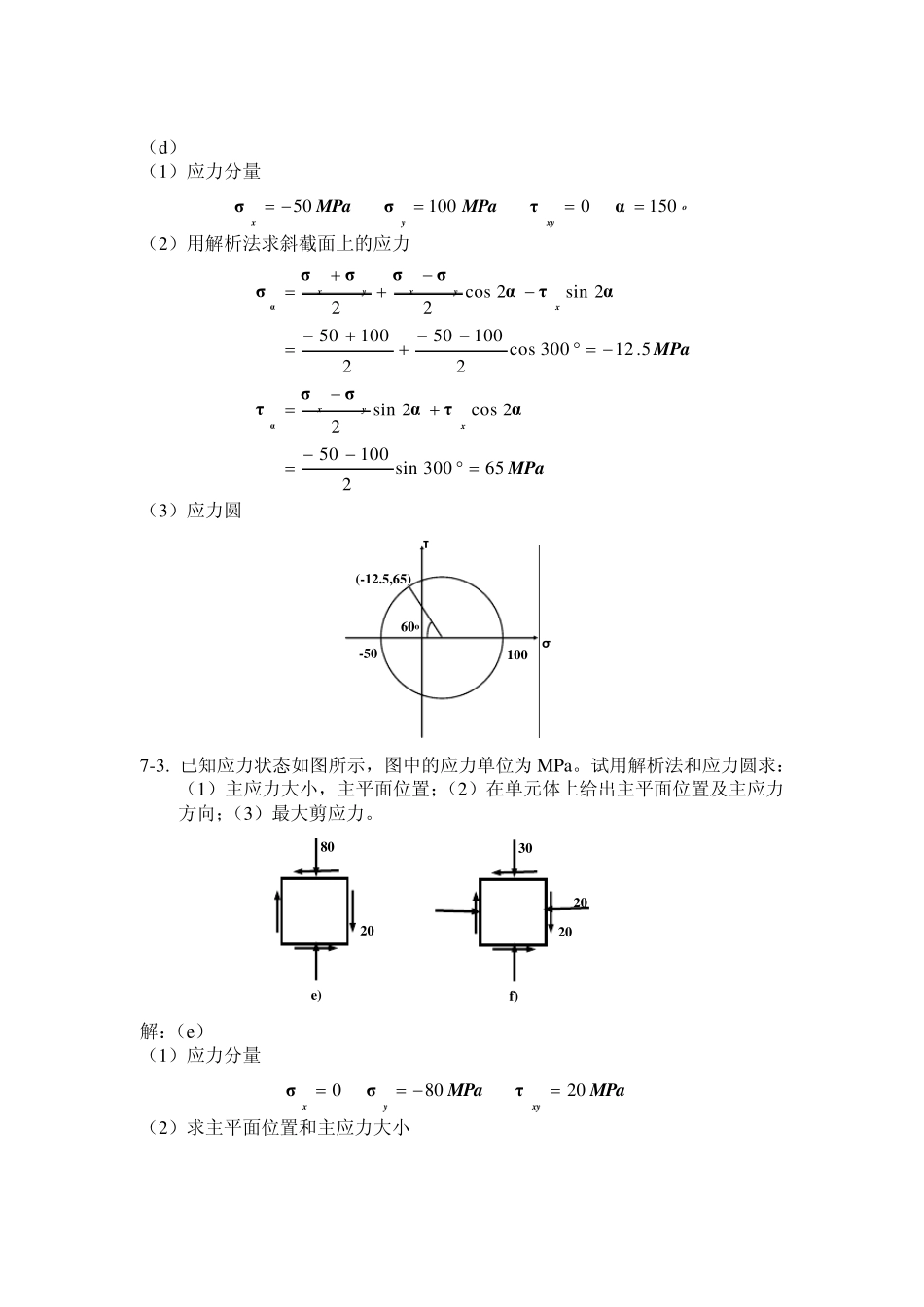
7-2. 在图示各单元体中，试用解析法和应力圆求斜面ab 上的应力。应力单位为MPa。 解：（a） （1）应力分量 oxyyxMPaMPa30 0 70 70ατσσ （2）用解析法求斜截面上的应力 MPaMPaxyyxxyyxyx6.6060sin270702cos2sin23560cos27070270702sin2cos22ατασστατασσσσσαα （3）应力圆 （b） （1）应力分量 oxyyxMPaMPa30 0 70 70ατσσ （2）用解析法求斜截面上的应力 70 70 a) 30o 50 100 c) 30o 50 100 d) 30o 70 70 b) 30o 70 -70 σ τ (35,60.6) 60o 02cos2sin270270702sin2cos22ατασστατασσσσσααxyxxyxyxMPa （3）应力圆：为一点圆 （c） （1）应力分量 oxyyxMPaMPa60 0 50 100ατσσ （2）用解析法求斜截面上的应力 MPaMPaxyxxyxyx7.21120sin2501002cos2sin25.62120cos2501002501002sin2cos22ατασστατασσσσσαα （3）应力圆 (7 0 ,0 ) σ τ 1 0 0 5 0 σ τ (6 2 .5 ,2 1 .7 ) 1 2 0 o （d） （1）应力分量 oxyyxMPaMPa150 0 100 50ατσσ （2）用解析法求斜截面上的应力 MPaMPaxyxxyxyx65300sin2100502cos2sin25.12300cos2100502100502sin2cos22ατασστατασσσσσαα （3）应力圆 7-3. 已知应力状态如图所示，图中的应力单位为MPa。试用解析法和应力圆求：（1）主应力大小，主平面位置；（2）在单元体上给出主平面位置及主应力方向；（3）最大剪应力。 解：（e） （1）应力分量 MPaMPaxyyx20 80 0τσσ （2）求主平面位置和主应力大小 20 80 e) 20 30 f) 20 100 -50 σ τ (-12.5,65) 60o oooyxxytg7.7690 3.135.022000αασστα MPaMPaMPaMPaxyxyx7.84 0 7.47.847.420)280(280)2(23212222minmaxσσστσσσσσσ （3）主平面位置及主应力方向 （4）最大剪应力 MPa7.4427.847.4231maxσστ （5）应力圆 （f） （1）应力分量 MPaMPaMPaxyyx20 30 20τσσ （2）求主平面位置和主应力大小 oooyxxytg3.10990 3.198.022000αασστα ...