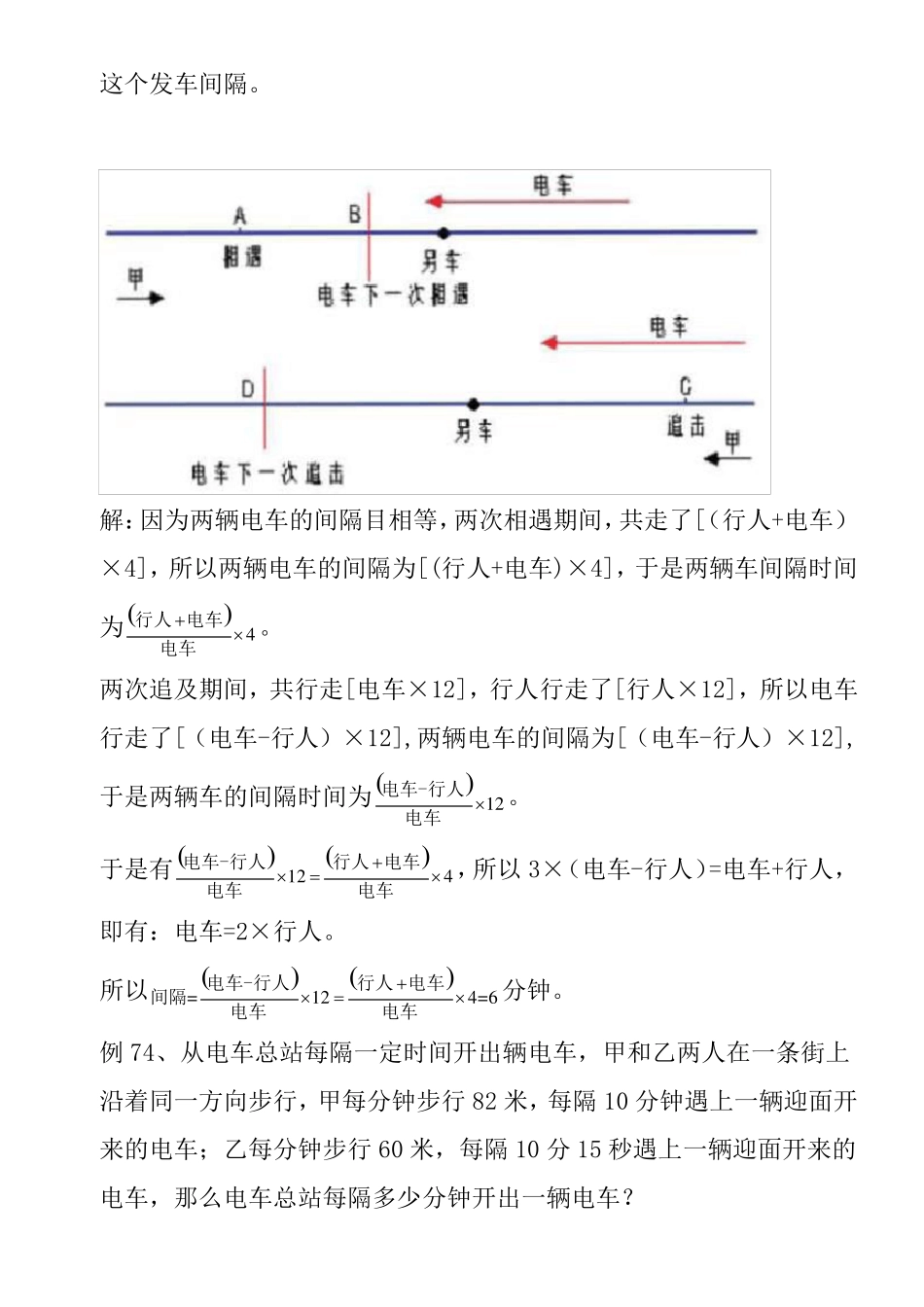
数学竞赛讲义之行程问题 多车相遇 例72 、一条电车线路的起点站和终点站分别是甲站和乙站,自隔5 分钟有一辆电车从甲站发出开往乙站,全程要走15 分钟,有一个人从乙 站出发沿着电车线路骑车前往甲站。他出发的时侯,恰好有一辆电车到达乙站。在路上他又遇到到了10 辆迎面开来的电车,到达甲站时,恰好又有一辆电车从甲站开出。问他从乙站到甲站用了多少分钟? 解:一辆车走完全程需要15 分钟,所以一辆车刚发出时,途中有 15÷3-1=2 辆车。 所以当人骑车出发时,而甲站车时,在中途有两辆车子,可以相遇,所以共相遇10 辆车,于是又发车8 辆相遇,恰到达时,又发车,于是发车9 辆时,甲到达,即有8 个时间间隔,时间为5×8=40 分钟。所以骑车行完全程的时间为40 分钟。 例73、某人沿电车路线行走,每隔12 分钟有一辆电车从后面追上,每4 分钟有一辆电车迎面开来。假设两个起点站的发车间隔是相同的。求这个发车间隔。 解:因为两辆电车的间隔目相等,两次相遇期间,共走了[(行人+电车)×4],所以两辆电车的间隔为[(行人+电车)×4],于是两辆车间隔时间为4行人电车电车 。 两次追及期间,共行走[电车×12],行人行走了[行人×12],所以电车行走了[(电车-行人)×12],两辆电车的间隔为[(电车-行人)×12],于是两辆车的间隔时间为12电车-行人电车 。 于是有124电车-行人 行人电车电车电车 ,所以 3×(电车-行人)=电车+行人,即有:电车=2×行人。 所以=124=6电车-行人 行人电车间隔电车电车分钟。 例 74、从电车总站每隔一定时间开出辆电车,甲和乙两人在一条街上沿着同一方向步行,甲每分钟步行82 米,每隔10 分钟遇上一辆迎面开来的电车;乙每分钟步行60 米,每隔10 分 15 秒遇上一辆迎面开来的电车,那么电车总站每隔多少分钟开出一辆电车? 假设甲、乙、电车共同相遇在A 点,甲、电车下一次相遇在C 点,乙、电车相遇在B 点。 则B 距A 点距离为BA=60 1061541米 C 距A 点距离为CA=82×10=820 米 所以 BC 两点相距的路程需电车10 分钟 15 秒-10 分钟=15 秒=41 分 路程为820 – 615=205 米 于是,电车的速度和为20582041米/分 于是,当 10 分钟前与甲、乙相遇的电车离甲(820 + 82)×10 = 9020米远。 两电车间隔为9020 米。所车间隔为9020÷820=11 分钟。 柳卡问题:这是一个著名的数学问题,由法国数学家...