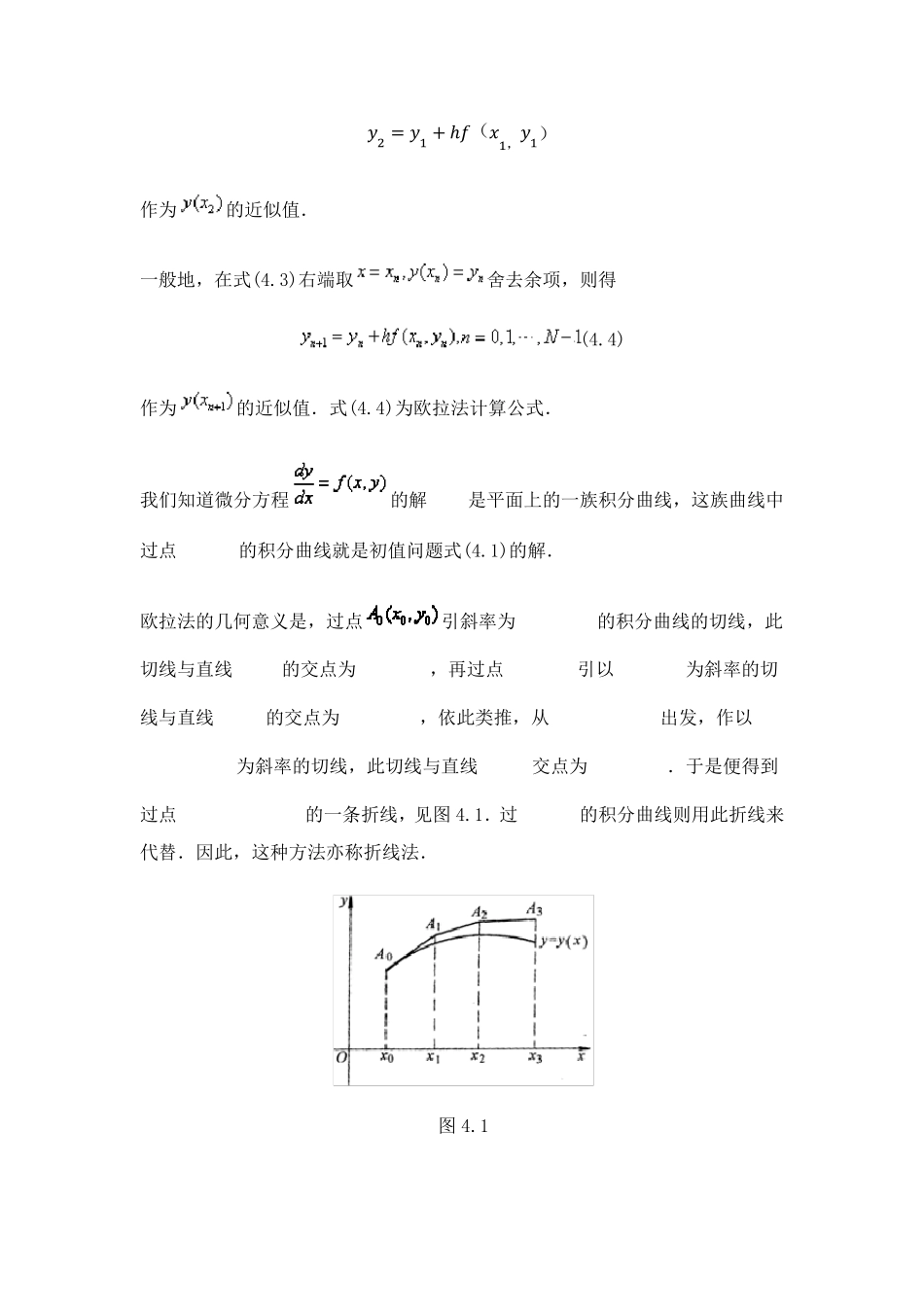
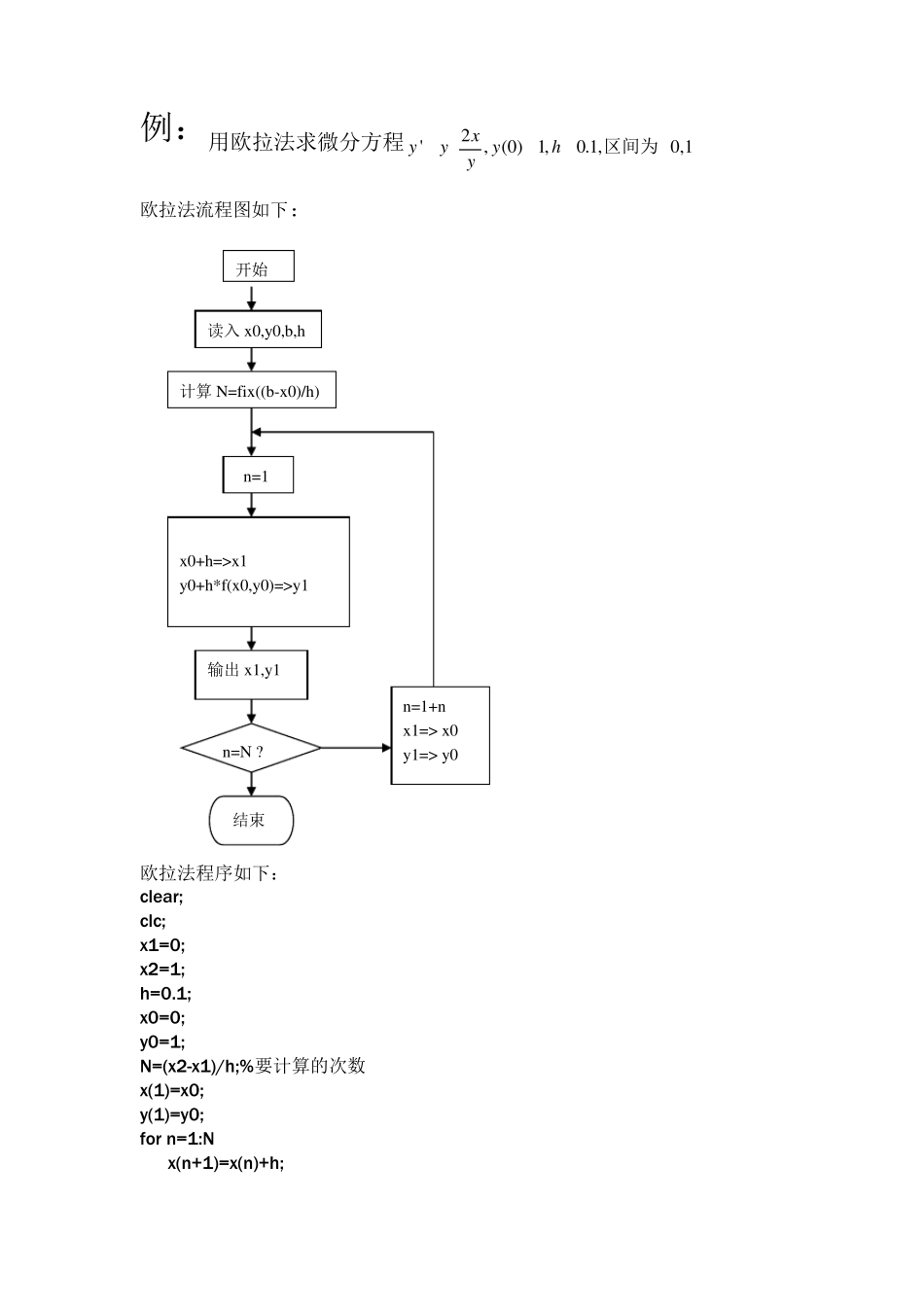
1 欧拉法求微分方程 方法说明 欧拉(Euler)法是解常微分方程初值问题 (4.1) 最简单的数值方法,其具体做法是,将区间[a,b]进行N 等分: ,步长 .并将式(4.1)写成等价的积分形 式 (4.2) 再对式(4.2)右端积分用矩形公式计算,则有 , (4.3) 在式(4.3)右端取,舍去余项。则得 , 作为的近似值。 在式(4.3)右端取,舍去余项,则得 ᵆ2 = ᵆ1 + ℎᵅ(ᵆ1,ᵆ1) 作为的近似值. 一般地,在式(4.3)右端取舍去余项,则得 (4.4) 作为 的近似值.式(4.4)为欧拉法计算公式. 我们知道微分方程的解是平面上的一族积分曲线,这族曲线中过点的积分曲线就是初值问题式(4.1)的解. 欧拉法的几何意义是,过点引斜率为的积分曲线的切线,此切线与直线的交点为,再过点引以为斜率的切线与直线的交点为,依此类推,从出发,作以为斜率的切线,此切线与直线交点为.于是便得到过点的一条折线,见图 4.1.过的积分曲线则用此折线来代替.因此,这种方法亦称折线法. 图 4.1 例:用欧拉法求微分方程[]2', (0) 1,0.1,0,1xyyyhy区间为= -== 欧拉法流程图如下: 欧拉法程序如下: clear; clc; x1=0; x2=1; h=0.1; x0=0; y0=1; N=(x2-x1)/h;%要计算的次数 x(1)=x0; y(1)=y0; for n=1:N x(n+1)=x(n)+h; x 0+h=>x 1 y 0+h*f(x 0,y 0)=>y 1 n =1 输出 x 1,y 1 n =1+n x 1=> x 0 y 1=> y 0 结束 n =N ? 读入 x 0,y 0,b,h 开始 计算 N=fix ((b-x 0)/h) y(n+1)=y(n)+h*(y(n)-2*x(n)/y(n)); end X=x Y=y 2 改进欧拉法求微分方程 方法说明 由于欧拉法采用矩形公式计算积分产生较大截断误差.改进欧拉法(又称改进折线法)是采取梯形公式来计算式(4.3)右端积分,则有 (5.1) 在式(5.1)右端取,舍去余项,则得 将作为的近似值. 在式(5.1)右端再取,舍去余项,则得 将作为的近似值. 一般地,在式(5.1)右端取,舍去余项.则得 (5.2) 将作为 的近似值. 式(5.2)为改进欧拉法计算公式. 流程图如下: 例:用改进欧拉法求微分方程[ ]2', (0 ) 1 ,0 .1 ,0 ,1xyyyhy区间为= -== 改进欧拉法程序如下: clear; clc; x1=0; x2=1; h=0.1; x0=0; y0=1; p(1)=0; N=(x2-x1)/h; x(1)=x0; y(1)=y0; for n=1:N x(n+1)=x(n)+h; y(n+1)=y(n)+h*(y(n)-2*x(n)/y(n)); p(n+1)=y(n)+h*(y(n+1)-2*x(n)/y(n+1)); y(n+1)=(y(n+1)+p(n+1))/2; end X=x Y=y 3 斐波那...