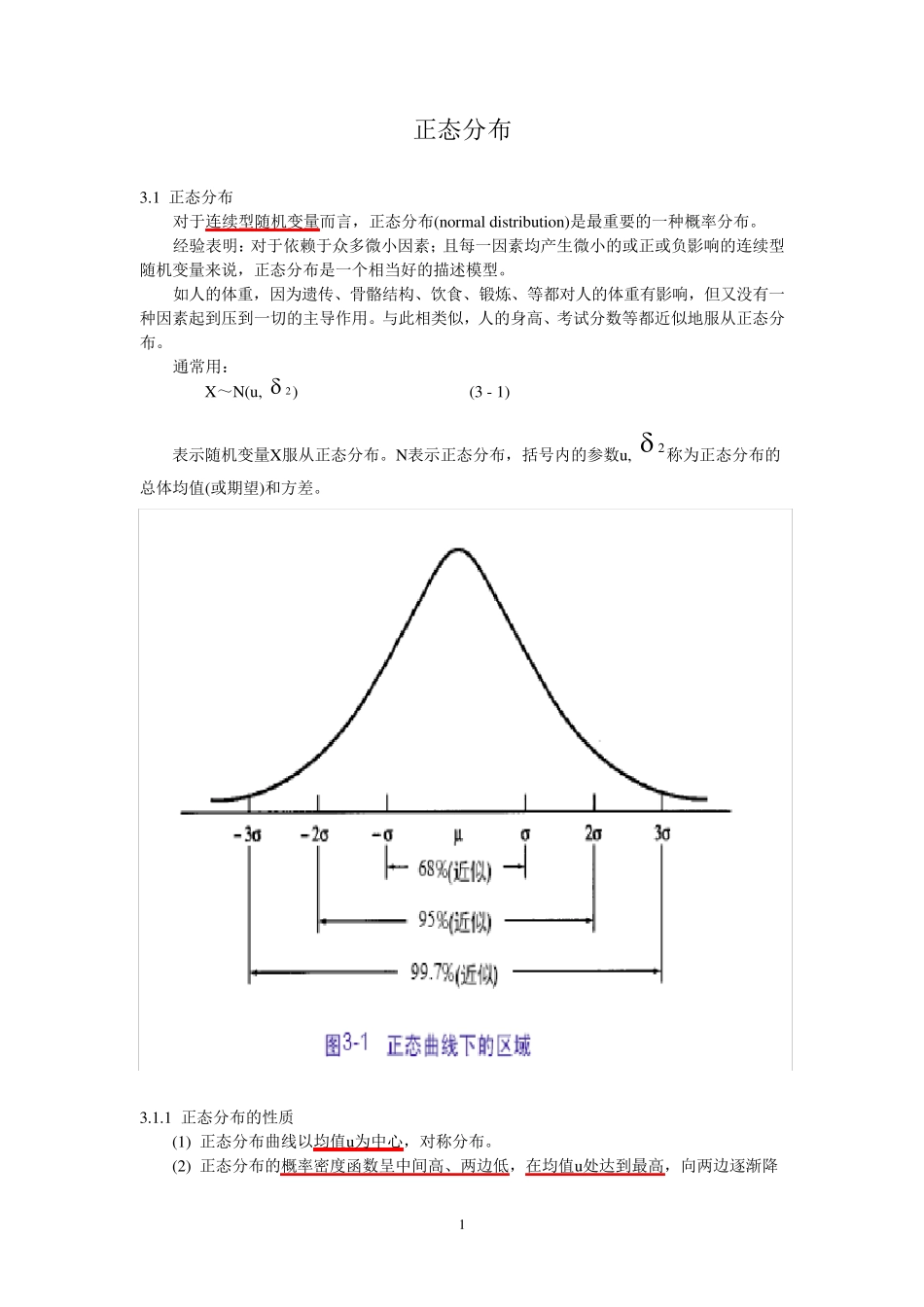
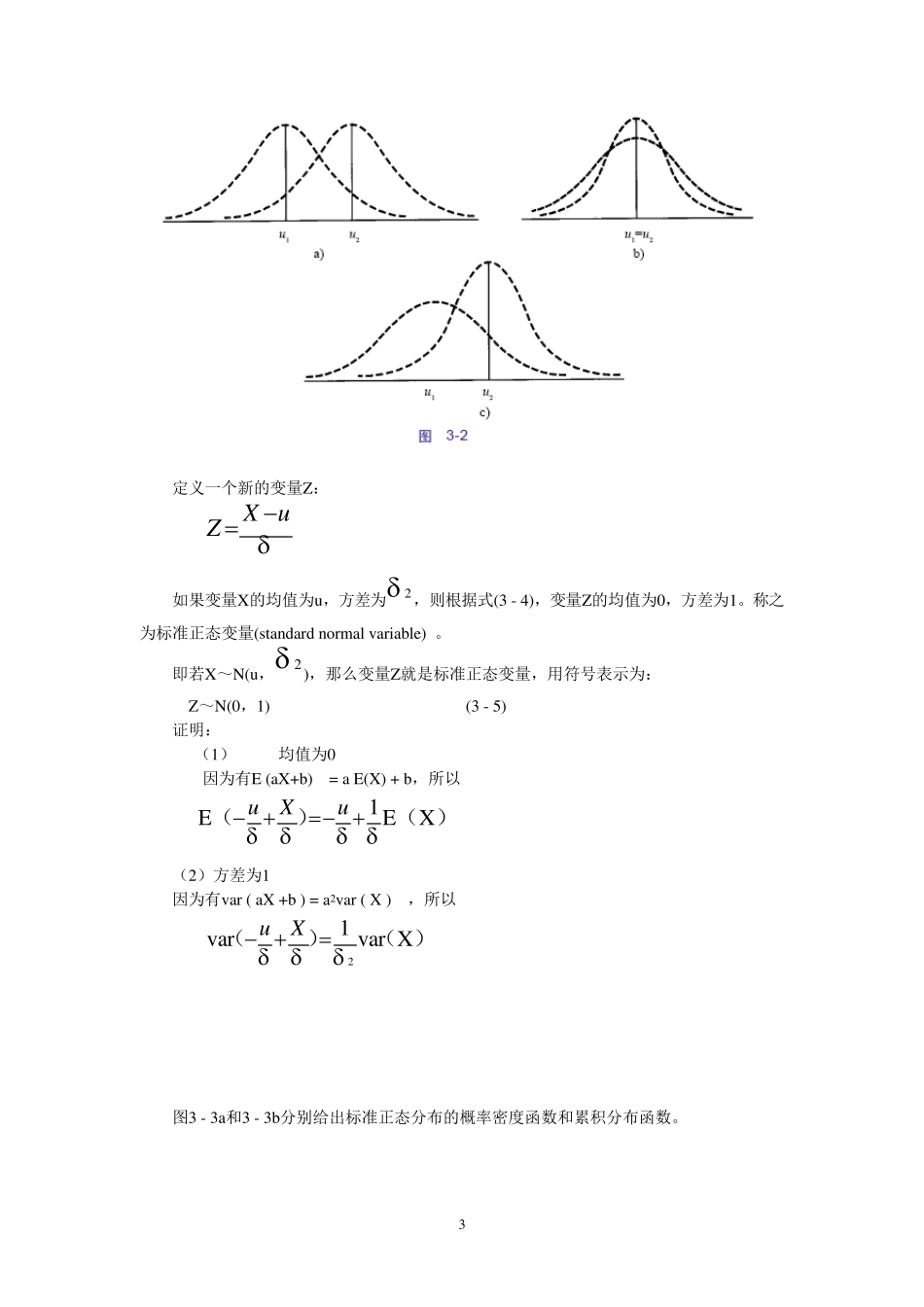
1 正态分布 3.1 正态分布 对于连续型随机变量而言,正态分布(normal distribu tion)是最重要的一种概率分布。 经验表明:对于依赖于众多微小因素;且每一因素均产生微小的或正或负影响的连续型随机变量来说,正态分布是一个相当好的描述模型。 如人的体重,因为遗传、骨骼结构、饮食、锻炼、等都对人的体重有影响,但又没有一种因素起到压到一切的主导作用。与此相类似,人的身高、考试分数等都近似地服从正态分布。 通常用: X~N(u , 2 ) (3 - 1) 表示随机变量X服从正态分布。N表示正态分布,括号内的参数u , 2 称为正态分布的总体均值(或期望)和方差。 3.1.1 正态分布的性质 (1) 正态分布曲线以均值u 为中心,对称分布。 (2) 正态分布的概率密度函数呈中间高、两边低,在均值u 处达到最高,向两边逐渐降 2 低,即随机变量在远离均值处取值的概率逐渐变小。 (3) 正态曲线下的面积约有68%位于u ± 两值之间;约有95%的面积位于u±22 之间;而约有99.7%的面积位于u±3 之间。 ★ (4) 两个(或多个)正态分布随机变量的线性组合仍服从正态分布。 令X和Y相互独立: X~N(uX,2x ) Y~N(uY,2y) 现在考虑两个变量的线性组合:W=a X+b Y 则 W~N(uW,2w ) ( 3 - 2 ) 其中, uW =(auX+buY) ( 3 - 3 ) 2w = (22xa +22yb ) (3 - 4) 例3.1 令X表示在下沙高教区一花店每日出售玫瑰花数量, Y表示在下沙镇一花店每日出售玫瑰花的数量,假定X和Y服从正态分布,且相互独立,并有: X~N( 100,64 ),Y~N( 150,81 ) 求两天内两花商出售玫瑰花数量的期望及方差? W=2X+2Y 根据式( 3 - 3 ) E(w)=E( 2X+ 2Y) = 5 0 0, Var (w) = 4var(X) + 4var(Y) = 5 8 0 因此,W服从均值为5 0 0,方差为5 8 0的正态分布,即W~N( 5 0 0,5 8 0 )。 ★★3.1.2 标准正态分布 两个正态分布可能因为期望或方差的不同,或是期望和方差均不同而相区别。如何比较各种不同的正态分布呢? 3 定义一个新的变量Z: X uZ 如果变量X的均值为u ,方差为2 ,则根据式(3 - 4),变量Z的均值为0,方差为1。称之为标准正态变量(standard normal v ariable) 。 即若X~N(u ,2),那么变量Z就是标准正态变量,用符号表示为: Z~N(0,1) (3 - 5) 证明: (1) 均值为0 因为有E (aX+b) = a E(X) + b,所以...