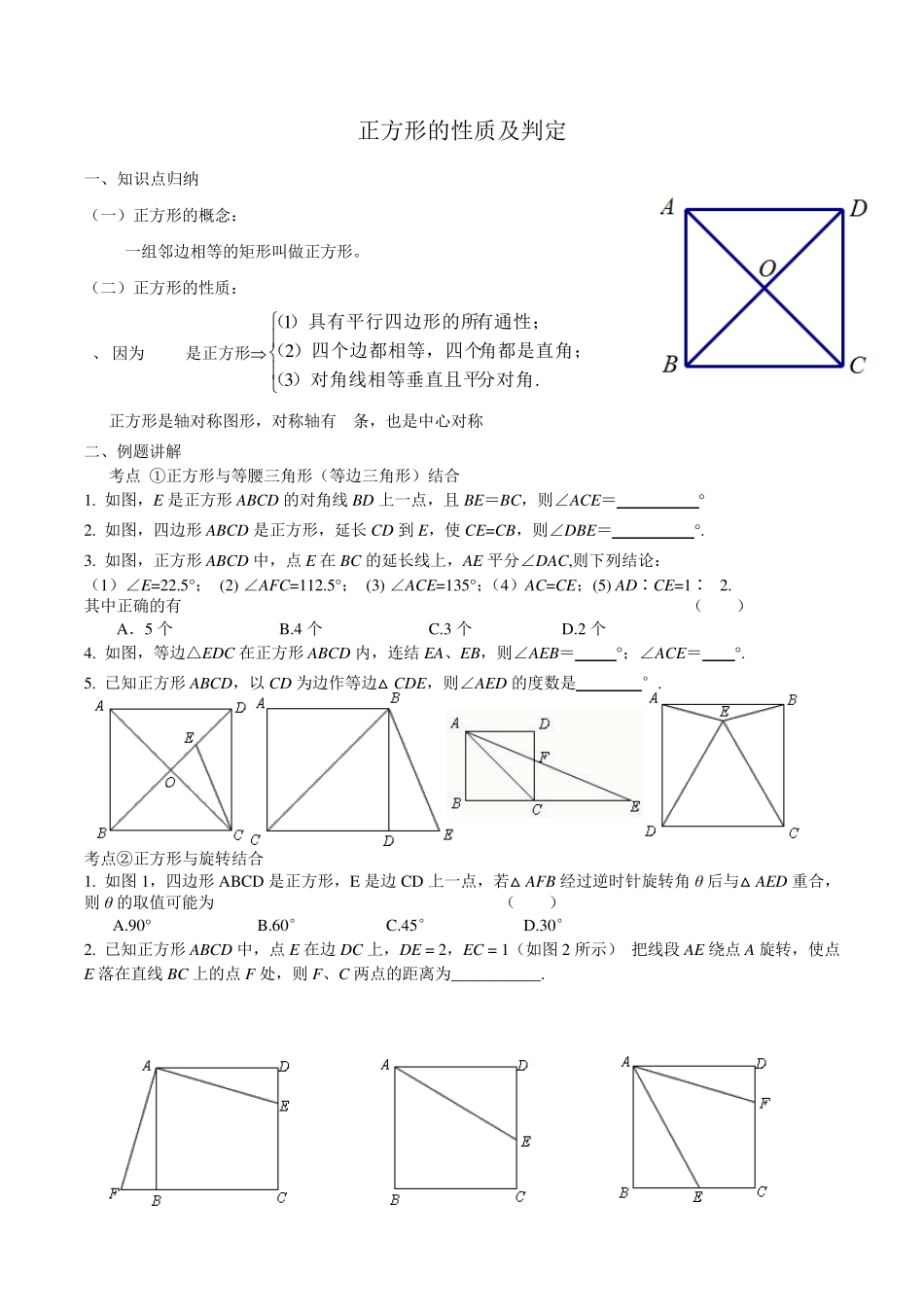
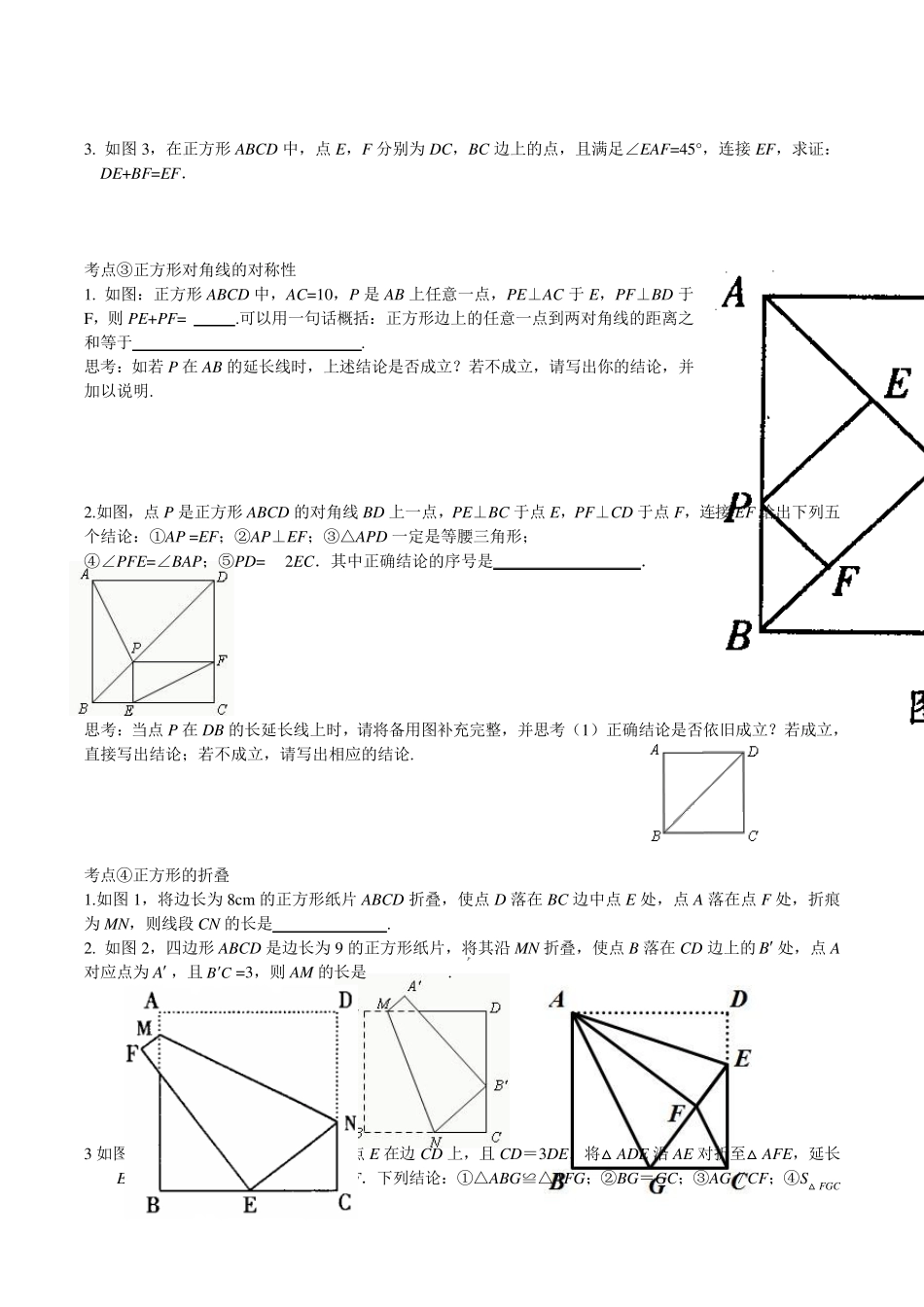
正方形的性质及判定 一、知识点归纳 (一)正方形的概念: 一组邻边相等的矩形叫做正方形。 (二)正方形的性质: 1、 因为ABCD是正方形.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所( 正方形是轴对称图形,对称轴有4条,也是中心对称 二、例题讲解 考点 ①正方形与等腰三角形(等边三角形)结合 1. 如图,E是正方形ABCD 的对角线BD 上一点,且BE=BC,则∠ACE= ° 2. 如图,四边形ABCD 是正方形,延长CD 到E,使CE=CB,则∠DBE= °. 3. 如图,正方形ABCD 中,点E在BC 的延长线上,AE平分∠DAC,则下列结论: (1)∠E=22.5°; (2) ∠AFC=112.5°; (3) ∠ACE=135°;(4)AC=CE;(5) AD∶CE=1∶2. 其中正确的有 ( ) A.5 个 B.4 个 C.3 个 D.2 个 4. 如图,等边△EDC 在正方形ABCD 内,连结EA、EB,则∠AEB= °;∠ACE= °. 5. 已知正方形ABCD,以CD 为边作等边△CDE,则∠AED 的度数是 °. 考点②正方形与旋转结合 1. 如图1,四边形ABCD 是正方形,E 是边CD 上一点,若△AFB 经过逆时针旋转角θ 后与△AED 重合,则θ 的取值可能为 ( ) A.90° B.60° C.45° D.30° 2. 已知正方形ABCD 中,点E在边DC 上,DE = 2,EC = 1(如图2 所示) 把线段 AE绕点A 旋转,使点E落在直线BC 上的点F处,则F、C 两点的距离为___________. 3. 如图3,在正方形ABCD 中,点E,F 分别为DC,BC 边上的点,且满足∠EAF=45°,连接 EF,求证:DE+BF=EF. 考点③正方形对角线的对称性 1. 如图:正方形ABCD 中,AC=10,P 是 AB 上任意一点,PE⊥AC 于 E,PF⊥BD 于F,则 PE+PF= .可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于 . 思考:如若 P 在AB 的延长线时,上述结论是否成立?若不成立,请写出你的结论,并加以说明. 2.如图,点P 是正方形ABCD 的对角线 BD 上一点,PE⊥BC 于点E,PF⊥CD 于点F,连接 EF 给出下列五个结论:①AP =EF;②AP⊥EF;③△APD 一定是等腰三角形; ④∠PFE=∠BAP;⑤PD= 2EC.其中正确结论的序号是 . 思考:当点P 在DB 的长延长线上时,请将备用图补充完整,并思考(1)正确结论是否依旧成立?若成立,直接写出结论;若不成立,请写出相应的结论. 考点④正方形的折叠 1.如图1,将边长为8cm 的正方形纸片 ABC...