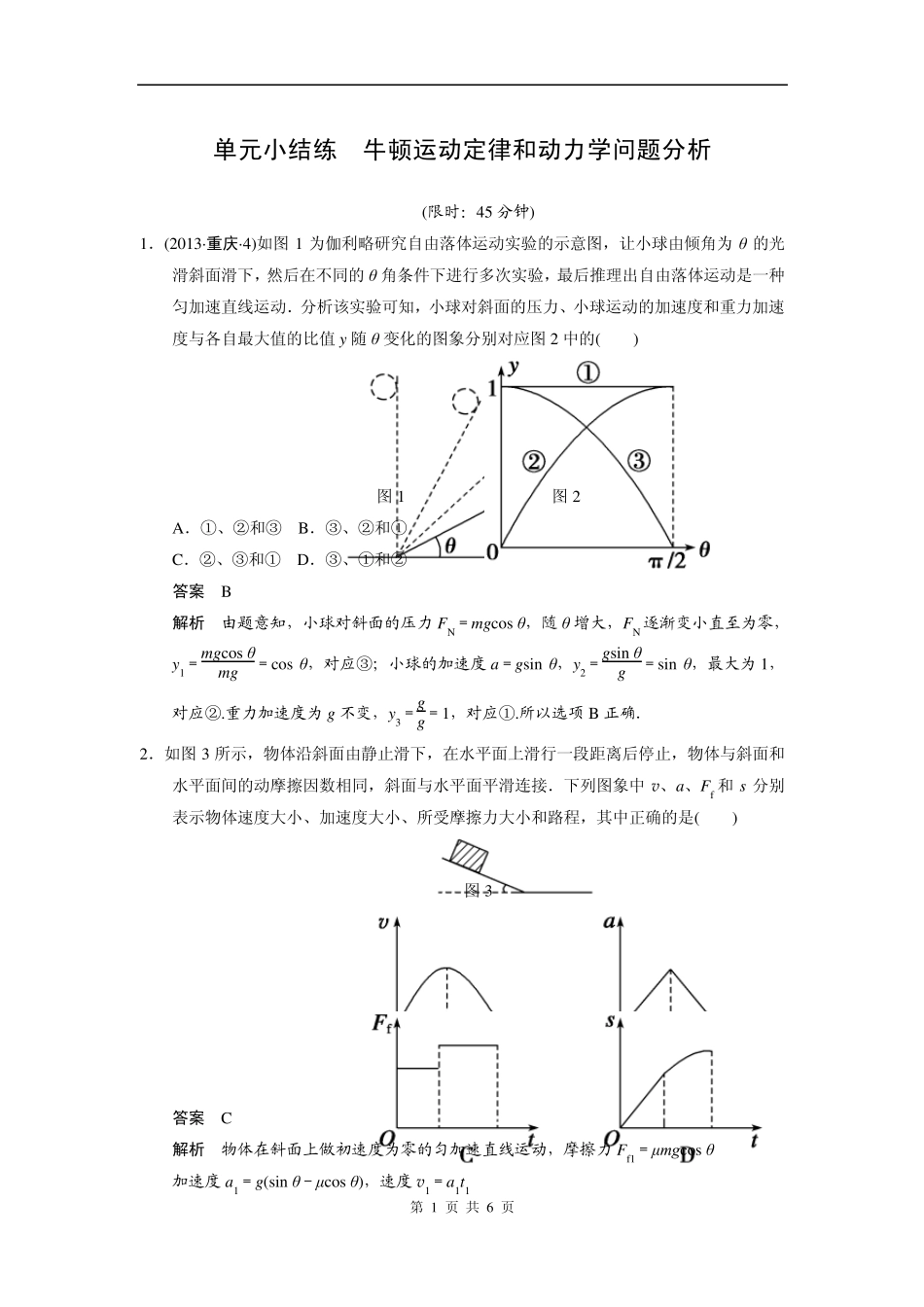
第 1 页 共 6 页 单元小结练 牛顿运动定律和动力学问题分析 (限时:45 分钟) 1.(2013·重庆·4)如图1 为伽利略研究自由落体运动实验的示意图,让小球由倾角为θ 的光滑斜面滑下,然后在不同的θ 角条件下进行多次实验,最后推理出自由落体运动是一种匀加速直线运动.分析该实验可知,小球对斜面的压力、小球运动的加速度和重力加速度与各自最大值的比值y 随θ 变化的图象分别对应图2 中的( ) 图1 图2 A.①、②和③ B.③、②和① C.②、③和① D.③、①和② 答案 B 解析 由题意知,小球对斜面的压力FN=mgcos θ,随θ 增大,FN 逐渐变小直至为零,y 1=mgcos θmg=cos θ,对应③;小球的加速度a=gsin θ,y 2=gsin θg=sin θ,最大为1,对应②.重力加速度为g 不变,y 3=gg=1,对应①.所以选项B 正确. 2.如图3 所示,物体沿斜面由静止滑下,在水平面上滑行一段距离后停止,物体与斜面和水平面间的动摩擦因数相同,斜面与水平面平滑连接.下列图象中v、a、Ff 和s 分别表示物体速度大小、加速度大小、所受摩擦力大小和路程,其中正确的是( ) 图3 答案 C 解析 物体在斜面上做初速度为零的匀加速直线运动,摩擦力Ff1=μmgcos θ 加速度a1=g(sin θ-μcos θ),速度v1=a1t1 第 2 页 共 6 页 路程s1=12a1t21,由此可知A、B、D 均错误; 在水平面上物体做匀减速直线运动,摩擦力 Ff2=μmg,加速度 a2=μg,速度 v2=v1-a2t2=a1t1-a2t2,所以 C 正确. 3.如图4(a)所示,一轻质弹簧的下端固定在水平面上,上端放置一物体(物体与弹簧不连接),初始时物体处于静止状态.现用竖直向上的拉力F 作用在物体上,使物体开始向上做匀加速运动,拉力F 与物体位移x 之间的关系如图(b)所示(g=10 m/s2),则下列结论正确的是( ) 图4 A.物体与弹簧分离时,弹簧处于压缩状态 B.弹簧的劲度系数为7.5 N/cm C.物体的质量为3 kg D.物体的加速度大小为5 m/s2 答案 D 解析 设物体的质量为 m,静止时弹簧的压缩量为 Δx ,由题图可知Δx =4 cm,由牛顿第二定律可得 kΔx =mg① 现用竖直向上的拉力 F 作用在物体上,使物体开始向上做匀加速运动,根据拉力 F 与物体位移 x 的关系可得 10 N=ma② 30 N-mg=ma③ 联立①②③可以解得,物体的质量 m=2 kg,物体的加速度 a=5 m/s2,k=500 N/m,故只有 D 正确. 4.如图5 所示,...