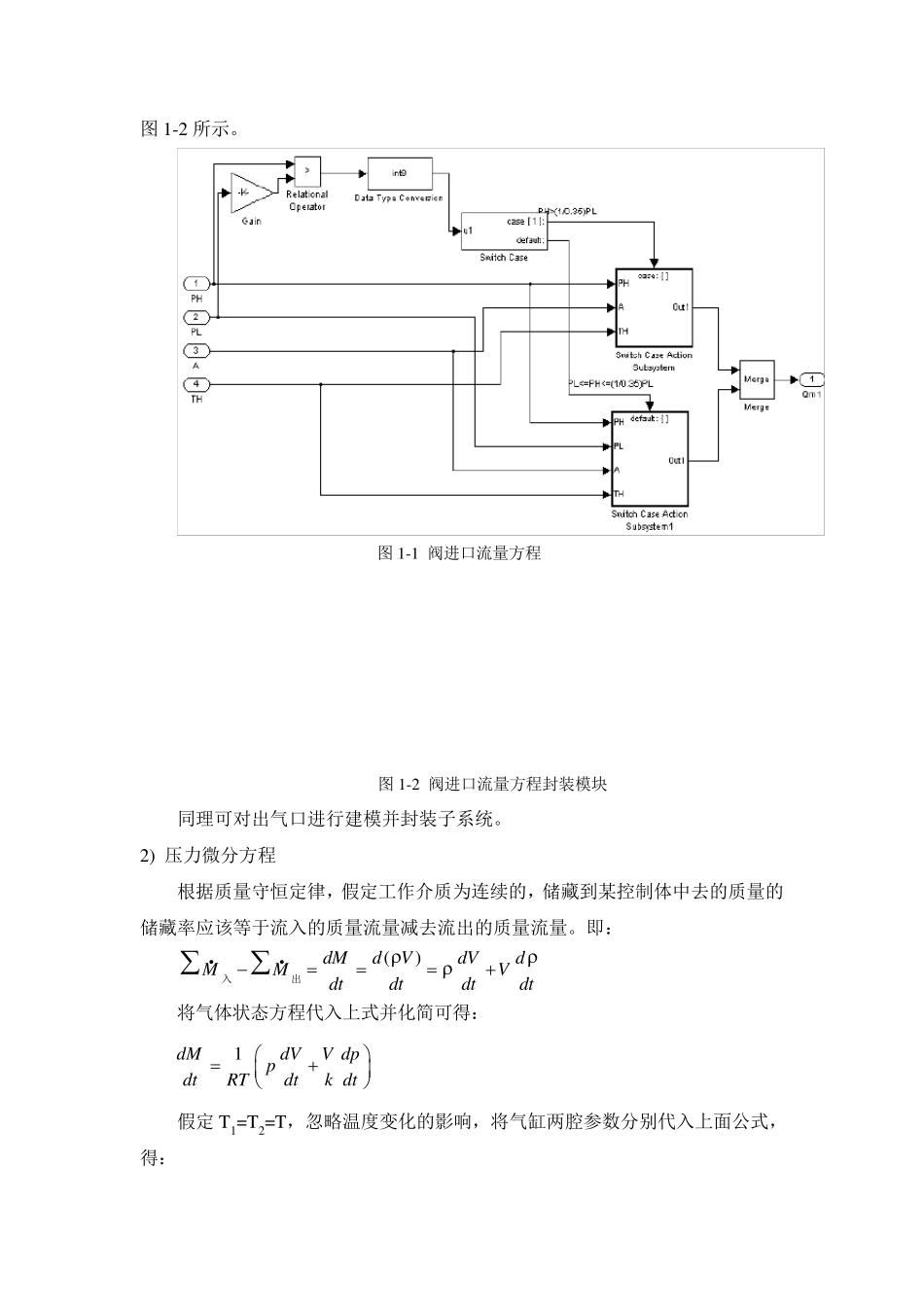
气压控制伺服系统的数学建模及仿真模型建立 关于气动伺服系统的数学建模,主要是通过分析系统的运动规律,运用一些己知的定理和定律,如热力学定律、能量守恒定律、牛顿第二定理等,通过一些合理而必要的假设和简化,推导出系统被控对象的基本状态方程,并将其在某一工作点附近线性化,从而获得的一个近似的数学模型。虽然这些模型不是很准确,但还是能够反映出气动伺服控制系统的受力和运动规律,并且借此可以分析出影响系统特性的主要因素,给系统的进一步分析和控制提供依据和指导。 另外,利用Simulink 工具包可以不受线性系统模型的限制,能够建立更加真实的非线性系统,同时其模型分析工具包括线性化和精简工具。因此,本文在数学模型的基础之上,利用Simulink 对所研究的气压力控制系统尝试建立一个非线性数学模型,并对该模型进行计算机仿真。 由于气动系统的非线性,如气体的压缩性较大,且在气缸的运动过程中容腔中气体的各参数和变量是实时变化的,所以对气动系统的精确建模是比较困难的。所以为了建立系统的模型,我们对控制系统作一些合理的假设,来简化系统的数学模型。假设如下: (1)气动系统中的工作介质—空气为理想气体; (2)忽略气缸与外界和气缸两腔之间的空气泄漏; (3)气动系统中的空气流动状态为等熵绝热过程; (4)气源压力和大气压力恒定; (5)同一容腔中的气体温度和压力处处相等。 1) 比例阀的流量方程 在实际的伺服控制系统中气体的流动过程十分复杂,气动元件研究中使用理想气体等熵通过喷管的流动过程来近似代替。一般计算阀口的流量时采用Sanville流量公式: kksdksdsmPPPPkRTkPq1212A 0.528