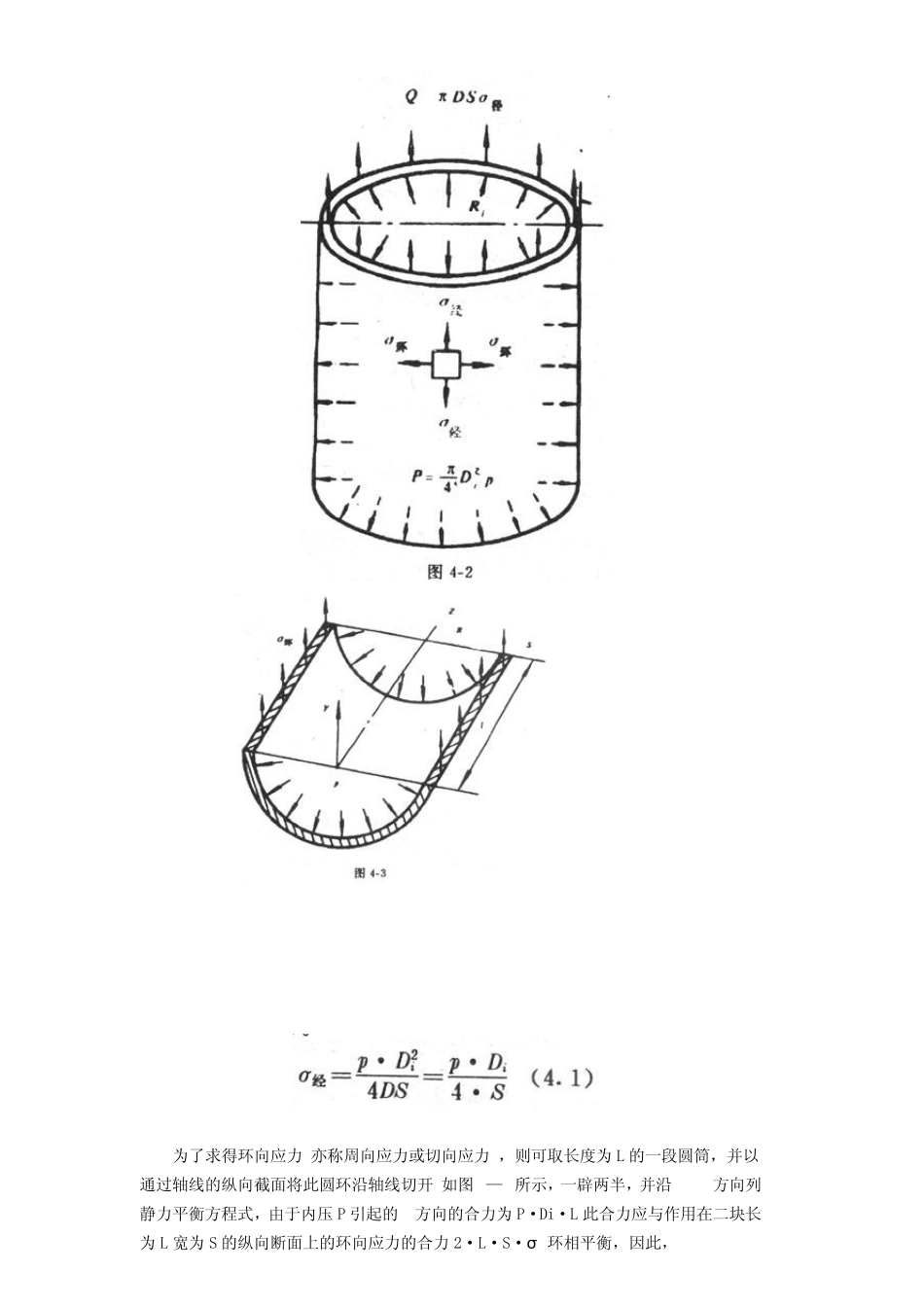
气瓶应力分析和强度计算 气瓶应力分析和强度计算 气瓶是一种承受内压的压力容器,一般由圆筒、封头、封底所组成。从受力情况看(这是强度设计的力学基础),它可以分为头部及其影响区、简体、底部及其影响区三部分。而强度设计的任务就是要正确确定每一部分的结构形状及其尺寸,保证在整个使用年限内安全运行。对已有的气瓶,则可利用应力分析及强度设计有关公式进行安全校验和剩余寿命的估算。图4—1 为一凹形底气瓶的应力分布图。 强度设计的基本原则是安全可靠,经济合理。 一、气瓶筒体的应力状态 气瓶筒体部分是一薄壁圆柱形壳体,或称薄壁圆筒。由于气瓶的公称工作压力可达30MPa,属于高压容器。制造气瓶的材料一般都选用强度较高的优质结构钢,所以其壁厚S相对于半径 Ri来说仍是很小的,一般S/Ri<1/10。根据力学分析及有关压力容器的设计规定,当圆筒外、内直径之比 Do/Di≤1.2时,可认为是薄壁圆筒,均可按薄壁圆筒设计。所谓薄壁圆筒,从力学上讲,就是指:当圆筒的壁厚相对于半径很小时,圆筒断面上承受弯矩的能力很小,筒壁主要承受拉力或压力,因此,可以近似地认为应力在整个筒壁上,沿壁厚度是均匀分布的,即所谓无力矩理论。按无力矩理论计算求得的应力称为薄膜应力。 现在我们来分析气瓶简体即薄壁圆筒的应力状态。 圆筒是最简单的一种回转壳体,也是压力容器中最基本的部分。薄壁圆筒的无力矩理论应力状态可以用分析回转壳体应力状态的一般方法求解,也可以更简单的从静力平衡方程式直接求得。以图4—2为例,如果我们在气瓶中部以垂直于轴线的平面(横截面)将气瓶截为上下二段,则作用在环断面的经向应力(亦称轴向应力)的合力为π DSo经,此力应与由内压P作用在气瓶底端的总轴向力(不管封头形状如何,均为π /4D2ip)相平衡, 即 因系薄壁圆筒,故内径 D”可近似地等于平均直径 Di.即 D1≈D,由此,可求得作用于圆筒横截面上的经向应力。 为了求得环向应力(亦称周向应力或切向应力),则可取长度为L 的一段圆筒,并以通过轴线的纵向截面将此圆环沿轴线切开,如图4—3所示,一辟两半,并沿Y--Y方向列静力平衡方程式,由于内压P 引起的Y方向的合力为P·Di·L 此合力应与作用在二块长为L 宽为S 的纵向断面上的环向应力的合力2·L·S·σ 环相平衡,因此, 公式(4.1)及(4.2)中圆筒的直径均为内径,所以有时亦称内径公式。如果式(4.1),(4.2)中Di近似地用平均直径D,则得中径公式: 对比式(4.1)及(4.2)...