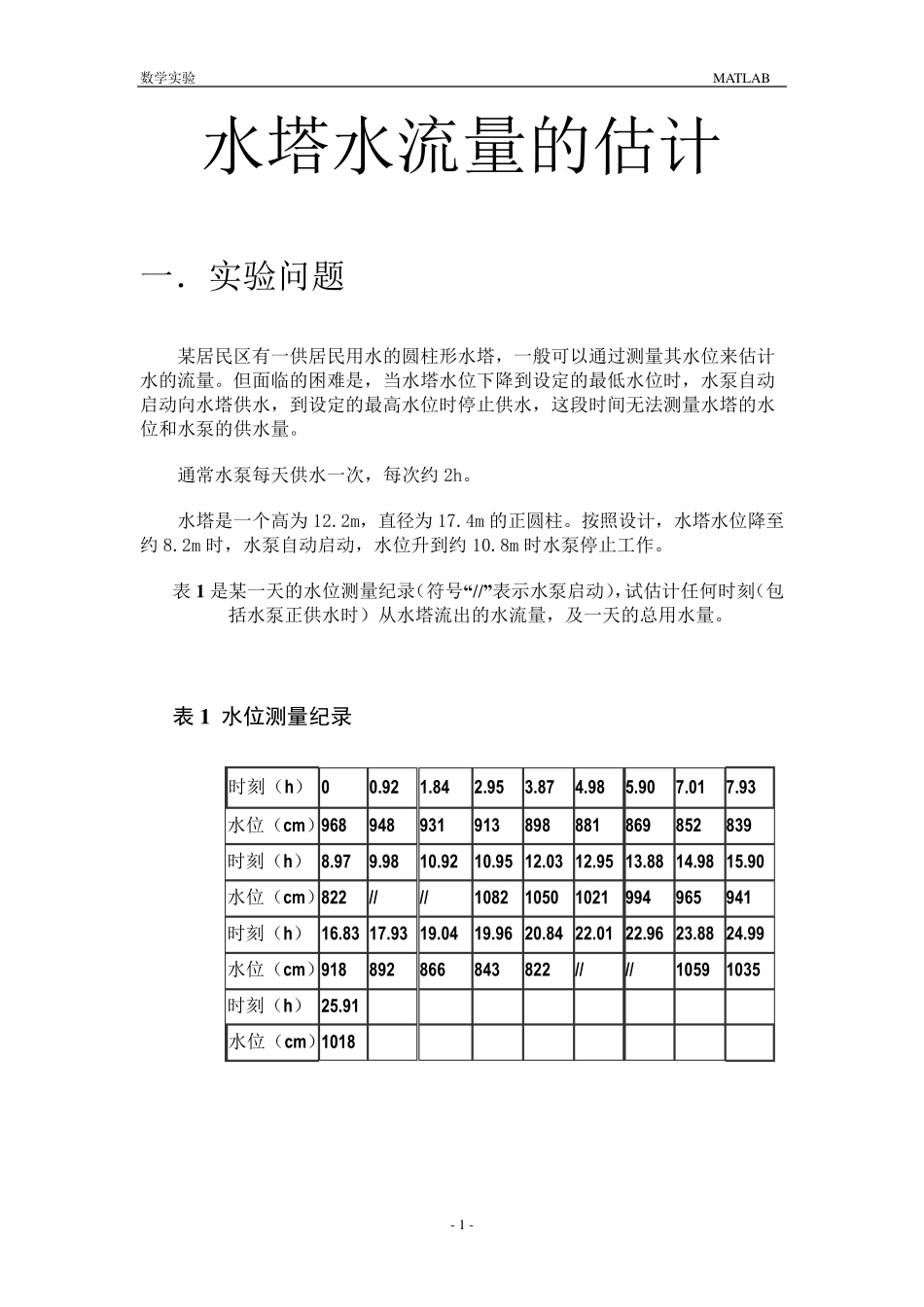
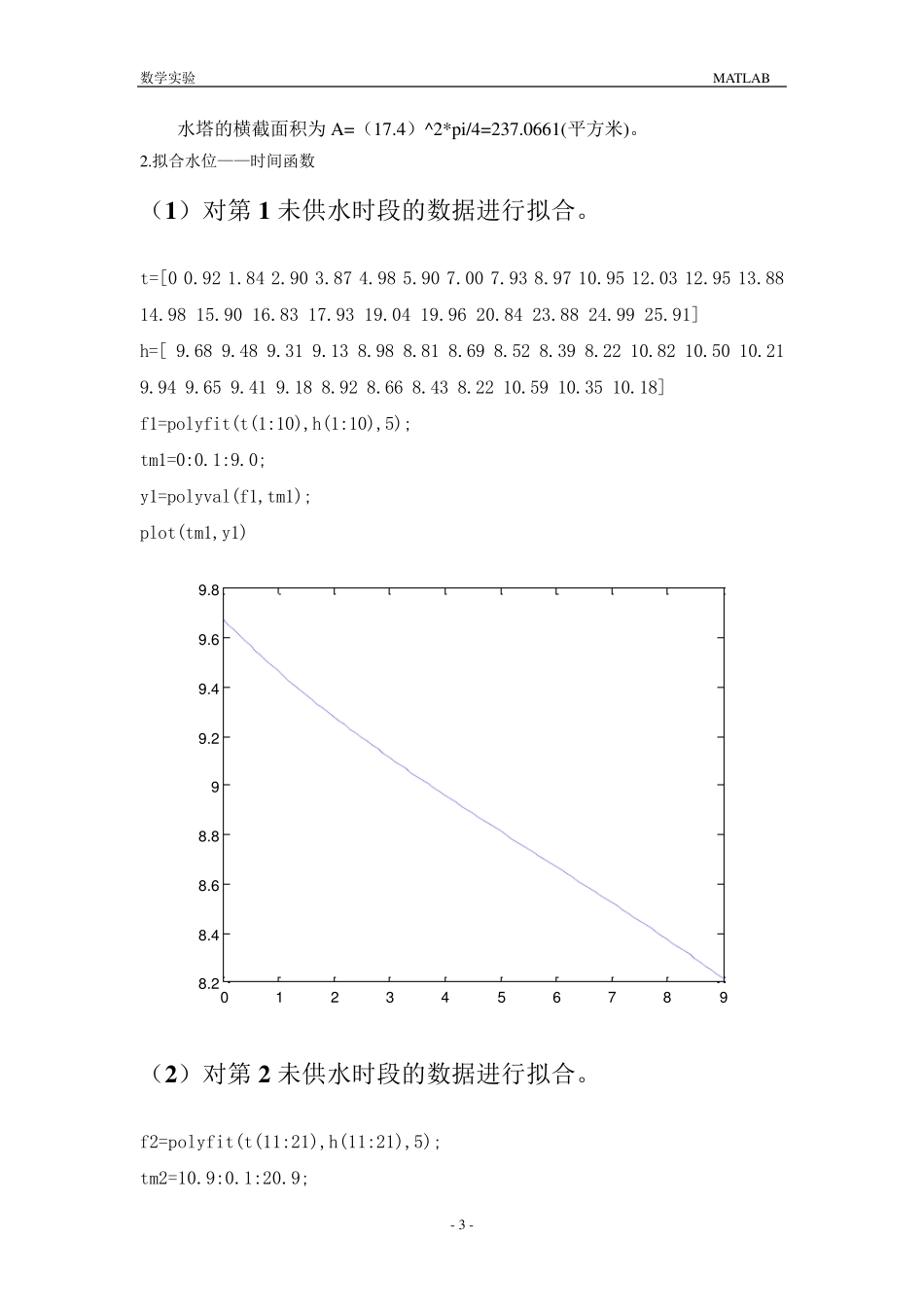
数学实验 MATLAB - 1 - 水塔水流量的估计 一.实验问题 某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量。但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量。 通常水泵每天供水一次,每次约 2h。 水塔是一个高为 12.2m,直径为 17.4m 的正圆柱。按照设计,水塔水位降至约 8.2m 时,水泵自动启动,水位升到约 10.8m 时水泵停止工作。 表 1 是某一天的水位测量纪录(符号“//”表示水泵启动),试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量。 表1 水位测量纪录 时刻(h) 0 0.92 1.84 2.95 3.87 4.98 5.90 7.01 7.93 水位(cm ) 968 948 931 913 898 881 869 852 839 时刻(h) 8.97 9.98 10.92 10.95 12.03 12.95 13.88 14.98 15.90 水位(cm ) 822 // // 1082 1050 1021 994 965 941 时刻(h) 16.83 17.93 19.04 19.96 20.84 22.01 22.96 23.88 24.99 水位(cm ) 918 892 866 843 822 // // 1059 1035 时刻(h) 25.91 水位(cm ) 1018 数学实验 MATLAB - 2 - 二.问题分析 根据以上数据的形式和以往经验,适合采用线性拟合的方式进行数据处理。对第1、2、3 未供水时段可直接进行用五次多项式进行拟合。对第1、2 供水时段分别在两端各取两个点用前后时刻的流速拟合得到。结果可以用分段函数表示分为 5 段,分别是第一未供水时段,第一供水时段,第二未供水时段,第二供水时段,第三未供水时段。 得出流速之后再乘以水塔横截面积即得任何时刻与水塔流出水流量的关系,即流速与时间的关系。对流速进行分段积分并求和,即得一天的总水流量。 三.程序的设计与求解方法 1 .数据的单位转换 时间(h) 水位(m ) 时间(h) 水位(m ) 0 9.68 12.95 10.21 0.92 9.48 13.88 9.93 1.84 9.31 14.98 9.65 2.95 9.13 15.90 9.41 3.87 8.98 16.83 9.18 4.98 8.81 17.93 8.92 5.90 8.69 19.04 8.66 7.00 8.52 19.96 8.43 7.93 8.39 20.84 8.22 8.97 8.22 22.02 水泵开启 9.98 水泵开启 22.90 水泵开启 10.93 水泵开启 23.88 10.59 10.95 10.82 24.99 10.35 12.03 10.50 25.91 10.18 数学实验 MATLAB - 3 - ...