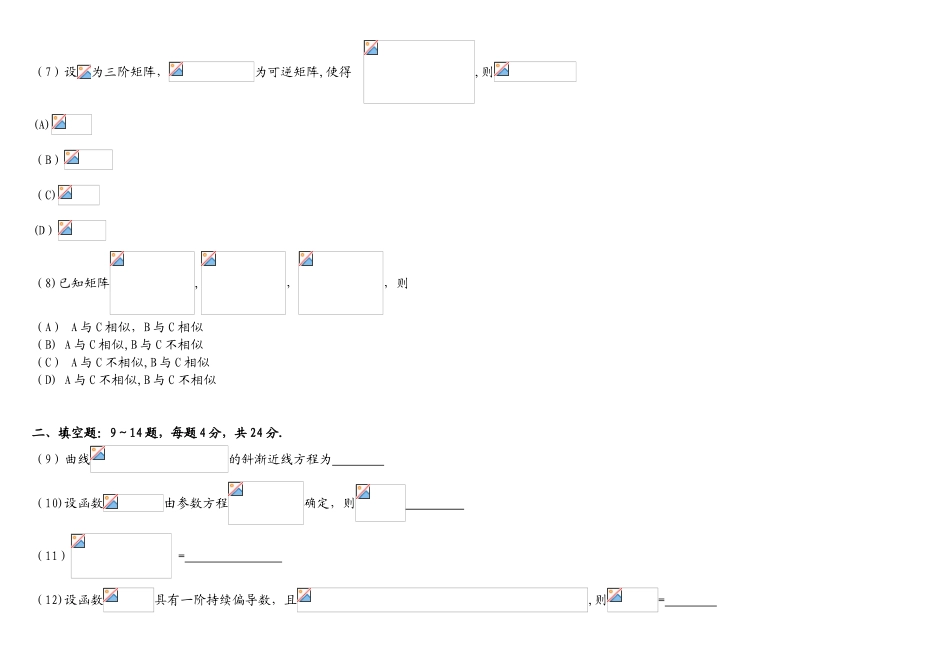
全国硕士硕士入学统一考试数学二试题一、选择题:1~8 小题,每题 4 分,共 32 分。下列每题给出的四个选项中,只有一种选项是符合题目规定的.(1)若函数在 x=0 持续,则(A) (B) (C) (D)(2)设二阶可到函数满足且,则(A) (B) (C) (D)(3)设数列收敛,则(A)当时, (B)当 时,则(C)当, (D)当时,(4)微分方程 的特解可设为 (A) (B)(C)(D)(5)设具有一阶偏导数,且在任意的,均有则(A) (B)(C)(D)(6)甲乙两人赛跑,计时开始时,甲在乙前方 10(单位:m)处,图中,实线表达甲的速度曲线 (单位:m/s)虚线表达乙的速度曲线,三块阴影部分面积的数值依次为 10,20,3,计时开始后乙追上甲的时刻记为(单位:s),则(A) (B) (C) (D)(7)设为三阶矩阵,为可逆矩阵,使得,则(A) (B)(C)(D)(8)已知矩阵,,,则(A) A 与 C 相似,B 与 C 相似 (B) A 与 C 相似,B 与 C 不相似 (C) A 与 C 不相似,B 与 C 相似 (D) A 与 C 不相似,B 与 C 不相似 二、填空题:9~14 题,每题 4 分,共 24 分.(9)曲线的斜渐近线方程为 (10)设函数由参数方程确定,则 (11) = (12)设函数具有一阶持续偏导数,且,则= (13) (14)设矩阵的一种特征向量为,则 三、解答题:15~23 小题,共 94 分。解答应写出文字阐明、证明过程或演算环节.(15)(本题满分 10 分)求(16)(本题满分 10 分)设函数具有 2 阶持续性偏导数,,求,(17)(本题满分 10 分)求(18)(本题满分 10 分)已知函数由方程确定,求的极值(19)(本题满分 10 分)在上具有 2 阶导数,,证明(1)方程在区间至少存在一种根(2)方程 在区间内至少存在两个不一样的实根(20)(本题满分 11 分)已知平面区域,计算二重积分(21)(本题满分 11 分)设是区间内的可导函数,且,点是曲线上的任意一点,在点处的切线与轴相交于点,法线与轴相交于点,若,求上点的坐标满足的方程。(22)(本题满分 11 分)三阶行列式有 3 个不一样的特征值,且 (1)证明(2)假如求方程组 的通解(23)(本题满分 11 分) 设在正交变换下的原则型为 求的值及一种正交矩阵.全国硕士硕士入学统一考试数学二试题一、选择:1~8 小题,每题 4 分,共 32 分.下列每题给出的四个选项中,只有一种选项是符合规定的。(1)设,,.当时,以上 3 个无穷小量按照从低阶到高阶拓排序是(A). (B)。(C). (D)。...