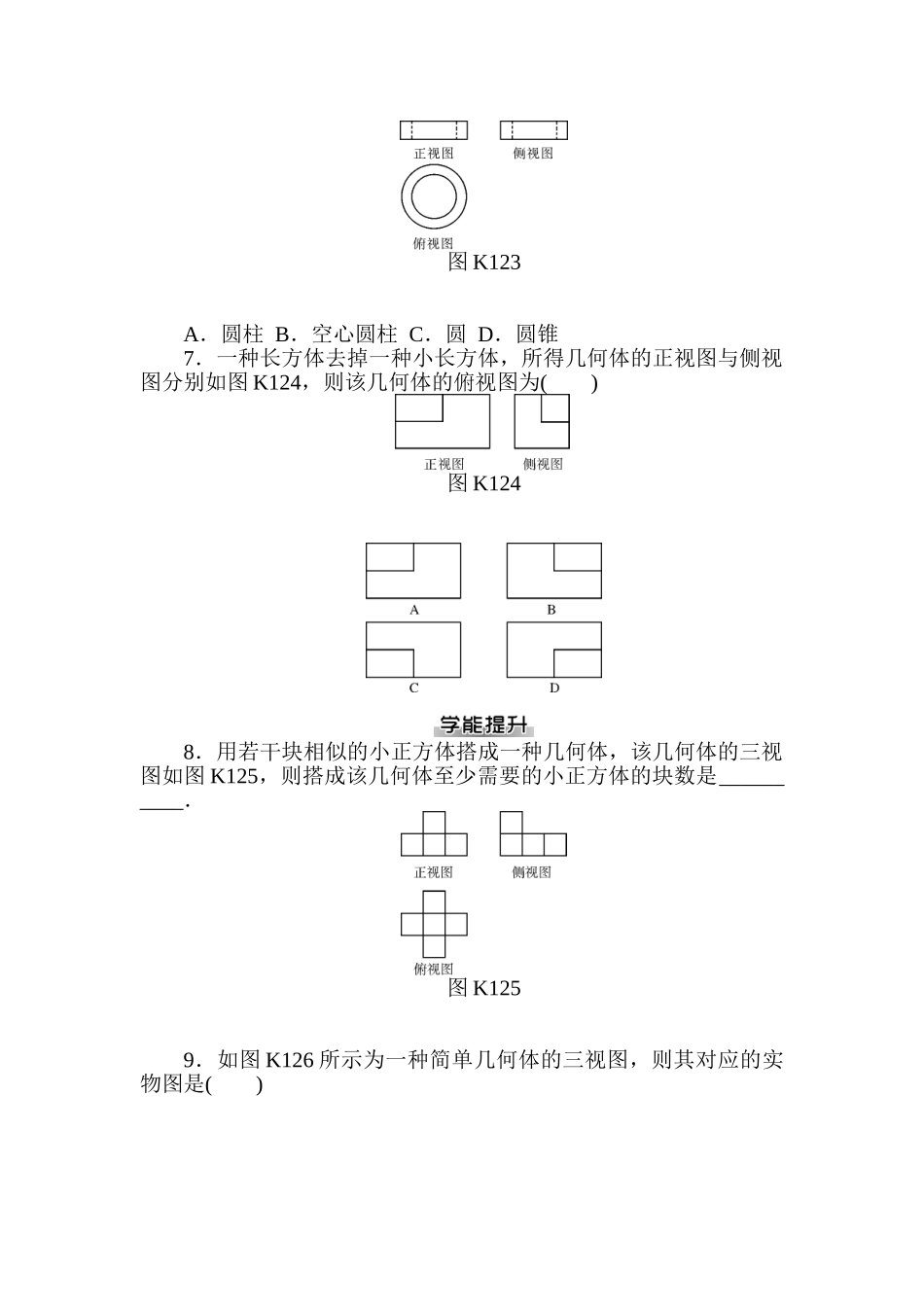
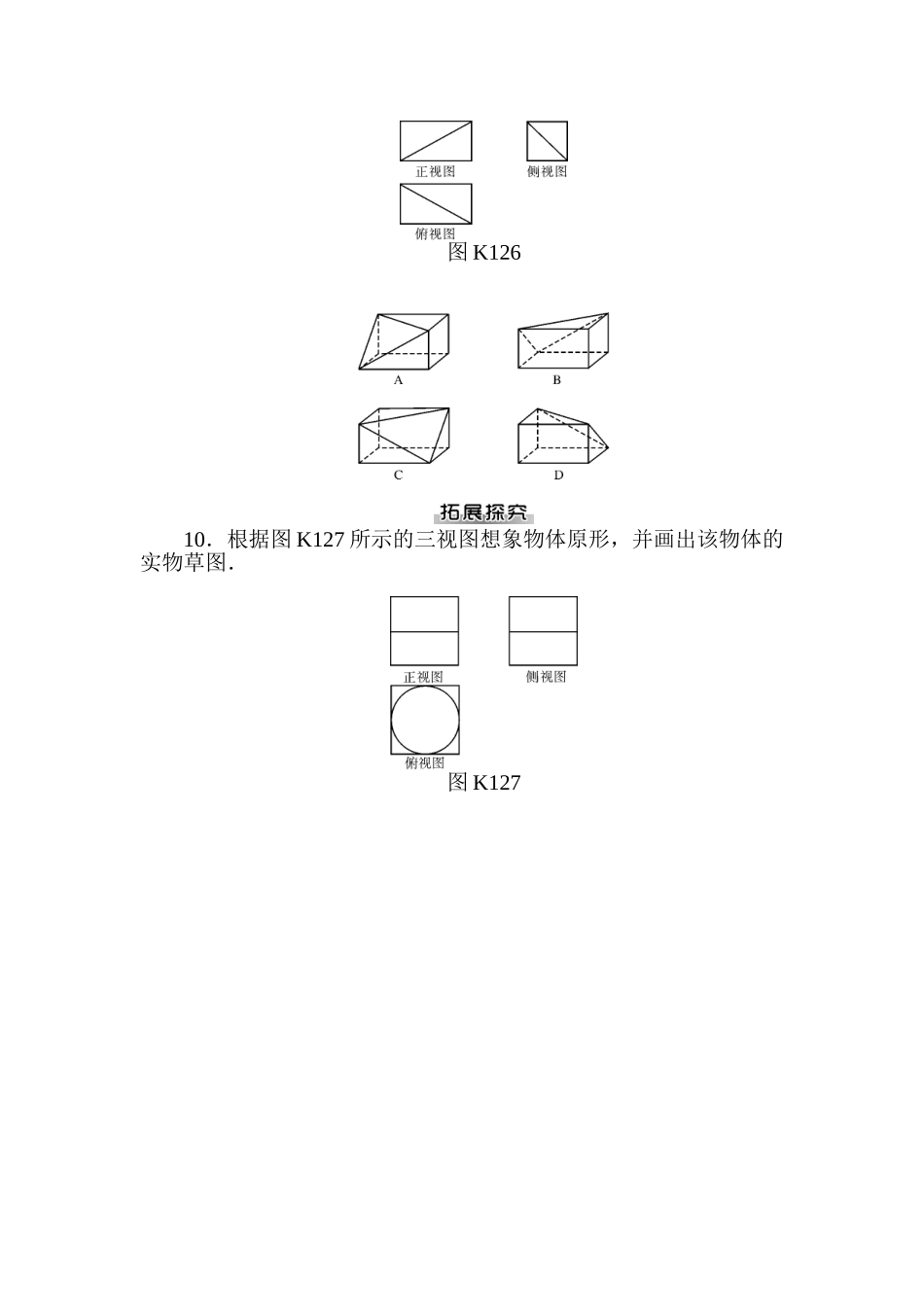
1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影及空间几何体的三视图 1. (四川)一种几何体的三视图如图 K121,则该几何体可以是( )图 K121A.棱柱 B.棱台C.圆柱 D.圆台2.两条不平行的直线,其平行投影不也许是( )A.两条平行直线 B.一点和一条直线C.两条相交直线 D.两个点3.下列几种有关投影的说法不对的的是( )A.平行投影的投影线是互相平行的B.中心投影的投影线是互相垂直的C.线段上的点在中心投影下仍然在线段上D.平行的直线在中心投影下不平行4.(湖南)已知正方体的棱长为 1,其俯视图是一种面积为 1 的正方形,侧视图是一种面积为的矩形,则该正方体的正视图的面积等于( )A. B.1 C. D.5.某几何体的三视图如图 K122,那么这个几何体是( )图 K122A.三棱锥 B.四棱锥 C.四棱台 D.三棱台6.图 K123 是某几何体的三视图,则这个几何体是( )图 K123A.圆柱 B.空心圆柱 C.圆 D.圆锥7.一种长方体去掉一种小长方体,所得几何体的正视图与侧视图分别如图 K124,则该几何体的俯视图为( )图 K1248.用若干块相似的小正方体搭成一种几何体,该几何体的三视图如图 K125,则搭成该几何体至少需要的小正方体的块数是__________.图 K1259.如图 K126 所示为一种简单几何体的三视图,则其对应的实物图是( )图 K12610.根据图 K127 所示的三视图想象物体原形,并画出该物体的实物草图.图 K1271.1.2 圆柱、圆锥、圆台、球及简单组合体的构造特征1.D 2.C 3.D4.D 解析:球的直径为长方体的体对角线长.5.B 6.一或无数多 7.①②③⑤8.2∶1 解析:可从底面入手,即圆内接一正三角形,正三角形内切一圆,易得答案.9.解:如图 D45 是几何体的轴截面,由题意知:AO=2 cm,A′O′=1 cm,SA=12 cm.由=,得 SA′=·SA=×12=6(cm).∴AA′=SA-SA′=6(cm).∴圆台的母线长为 6 cm. 图 D45 图 D4610.解:如图 D46,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为 x,则 OC=x,∴=,解得 x=,∴正方体的棱长为 cm.1.2 空间几何体的三视图和直观图1.2.1 中心投影与平行投影及空间几何体的三视图1.D 2.D 3.B 4.D 5.B 6.B 7.C8.6 9.A10.解:根据三视图想象物体原形如图 D47.图 D47