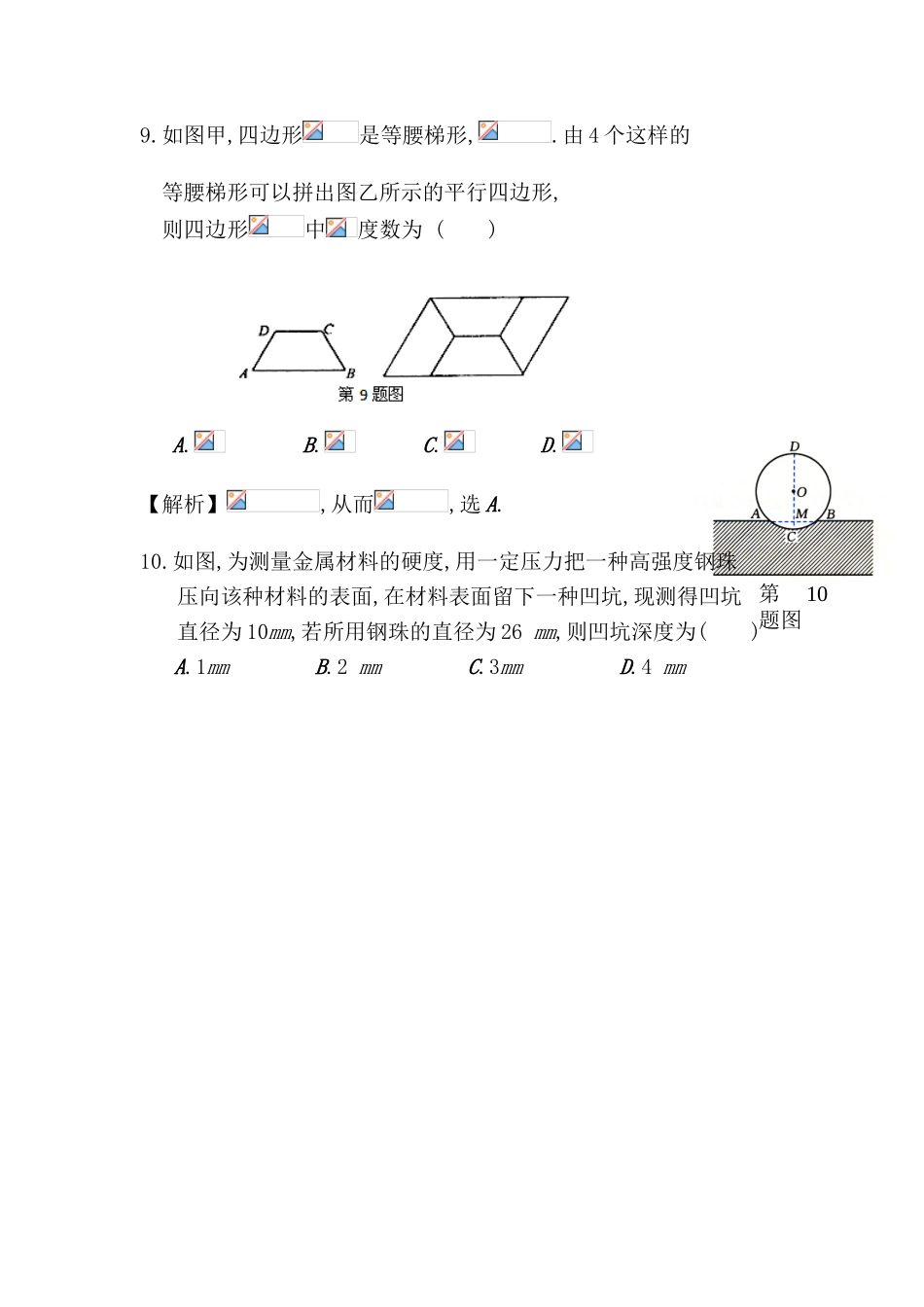
1.如图 4 所示,圆 O 的直径 AB=6,C 为圆周上一点,BC=3 过 C 作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC =( )A. B. C. D.C. D.,则的半径为( )第 6 题图A.4 B. C. D.8【解析】设半径为 ,由割线定理有,解得.故选 D.6.如图,是半圆的直径,点在半圆上,于点,且,设,则=( )A. B. C. D.8.半径分别为 1 和 2 的两圆外切,作半径为 3 的圆与这两圆均相切,一共可作( )个. A.2 B.3 C.4 D.5【解析】一共可作 5 个,其中均外切的 2 个,均内切的 1 个,一外切一内切的 2 个,故选 D.第10题图9.如图甲,四边形是等腰梯形,.由 4 个这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形中度数为 ( )A. B. C. D.【解析】,从而,选 A.10.如图,为测量金属材料的硬度,用一定压力把一种高强度钢珠压向该种材料的表面,在材料表面留下一种凹坑,现测得凹坑直径为 10mm,若所用钢珠的直径为 26 mm,则凹坑深度为( ) A.1mm B.2 mm C.3mm D.4 mm【解析】用平面截圆柱,截线椭圆的短轴长为圆柱截面圆的直径,弄清了这一概念,考虑椭圆所在平面与底面成角,则离心率.故选 A.13.一平面截球面产生的截面形状是_______;它截圆柱面所产生的截面形状是________【解析】圆;圆或椭圆.14.如图,在△ABC 中,AB=AC,∠C=720,⊙O 过A、B 两点且与 BC 相切于点 B,与 AC 交于点 D,连结 BD,第 15 题图若 BC=,则 AC= 【解析】由已知得,,解得.15.如图,为的直径,弦、交于点,若,则= 【解析】连结,则,又,从而,因此.16.如图为一物体的轴截面图,则图中 R 的值是 【解析】由图可得,解得.三、解答题:本大题共 6 小题,共 74 分.解答应写出文字阐明、证明过程或演算环节.17.(本小题满分 12 分) 如图:是的两条切线,是切点,是上两点,假如,试求的度数.【解析】连结,根据弦切角定理,可得 .19.(本小题满分 12 分)已知:如右图,在等腰梯形 ABCD 中,AD∥BC,AB=DC,过点 D 作 AC 的平行线 DE,交 BA 的延长线于点 E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.【解析】证明:(1) 四边形 ABCD 是等腰梯形,∴AC=DB AB=DC,BC=CB,∴△ABC≌△BCD(2) △ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB第21题图ODGCAEFBP∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.又, ∴,命题得证.21.(本小题满分 1...