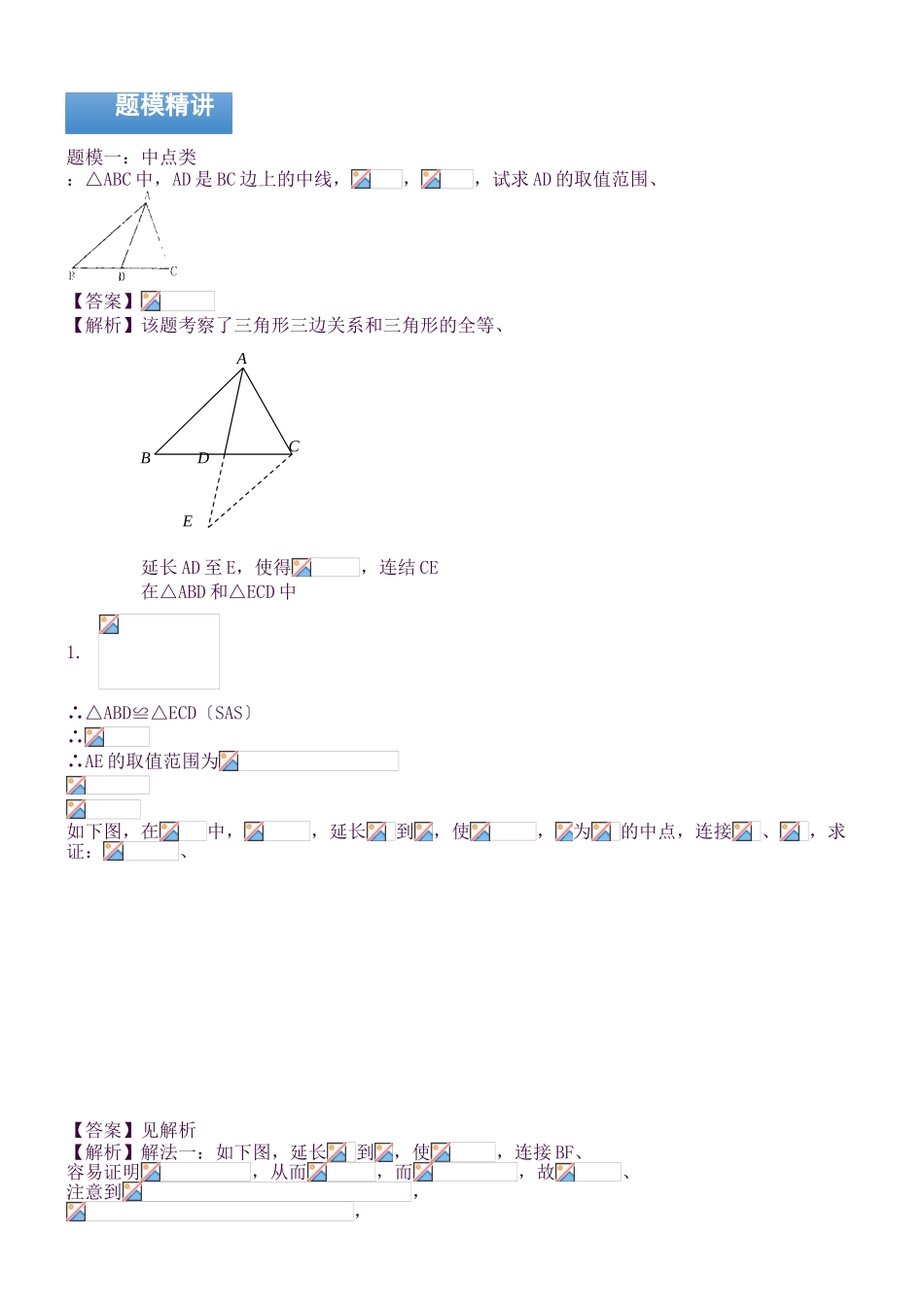
(第一章全等三角形的辅助线)知识点与练习含解析解析一、中点类辅助线作法见到中线(中点),我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段,尤其是在波及线段的等量关系时,倍长中线的应用更是较为常见,常见添加措施如下图〔是底边的中线)、二、角平分线类辅助线作法有如下三种作辅助线的方式:1、由角平分线上的一点向角的两边作垂线;2、过角平分线上的一点作角平分线的垂线,从而形成等腰三角形;3、,这种对称的图形应用得也较为普遍、三、截长补短类辅助线作法截长补短法,是初中数学几何题中一种辅助线的添加措施,也是把几何题化难为易的一种思想、所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段等于的两条较短线段中的一条,然后证明其中的另一段与的另一条线段相等;所谓“补短”,就是将一种的较短的线段延长至与另一种的较短的长度相等,然后求出延长后的线段与最长的线段的关系、有的是采用截长补短后,使之构成某种特定的三角形进行求解、一、考点:全等三角形辅助线的作法二、重难点:中点类、角平分线类、截长补短类辅助线作法三、易错点:1、辅助线只是一种指导措施,出现有关条件或结论时不一定要作辅助线或者是按照模型作辅助线,关键是怎样分析题目;2、辅助线不是随便都可以作的,例如“作一条线段等于此外一条线段且与某条线段夹角是多少度”这种辅助线就不一定能作出来、知识精讲三点剖析题模一:中点类:△ABC 中,AD 是 BC 边上的中线,,,试求 AD 的取值范围、【答案】【解析】该题考察了三角形三边关系和三角形的全等、延长 AD 至 E,使得,连结 CE在△ABD 和△ECD 中1.∴△ABD≌△ECD〔SAS〕∴∴AE 的取值范围为如下图,在中,,延长到,使,为的中点,连接、,求证:、【答案】见解析【解析】解法一:如下图,延长到,使,连接 BF、容易证明,从而,而,故、注意到,,题模精讲ABCDE故,而公用,故,因此、解法二:如下图,取的中点,连接、由于是的中点,是的中点,故是的中位线,从而,由可得,故,从而,、题模二:角平分线类如图,,平分,平分,点在上、① 探讨线段、和之间的等量关系、② 探讨线段与之间的位置关系、【答案】见解析【解析】①;②、证明如下:在线段上取点,使,连结、在和中∴∴, 而∴在和中∴∴,∴,如图,,,BD 为∠ABC 的平分线,CE⊥BE,求证:、【答案】见解析【解析】延长 CE,交 BA 的延长线于点 F、 BD 为∠ABC 的...