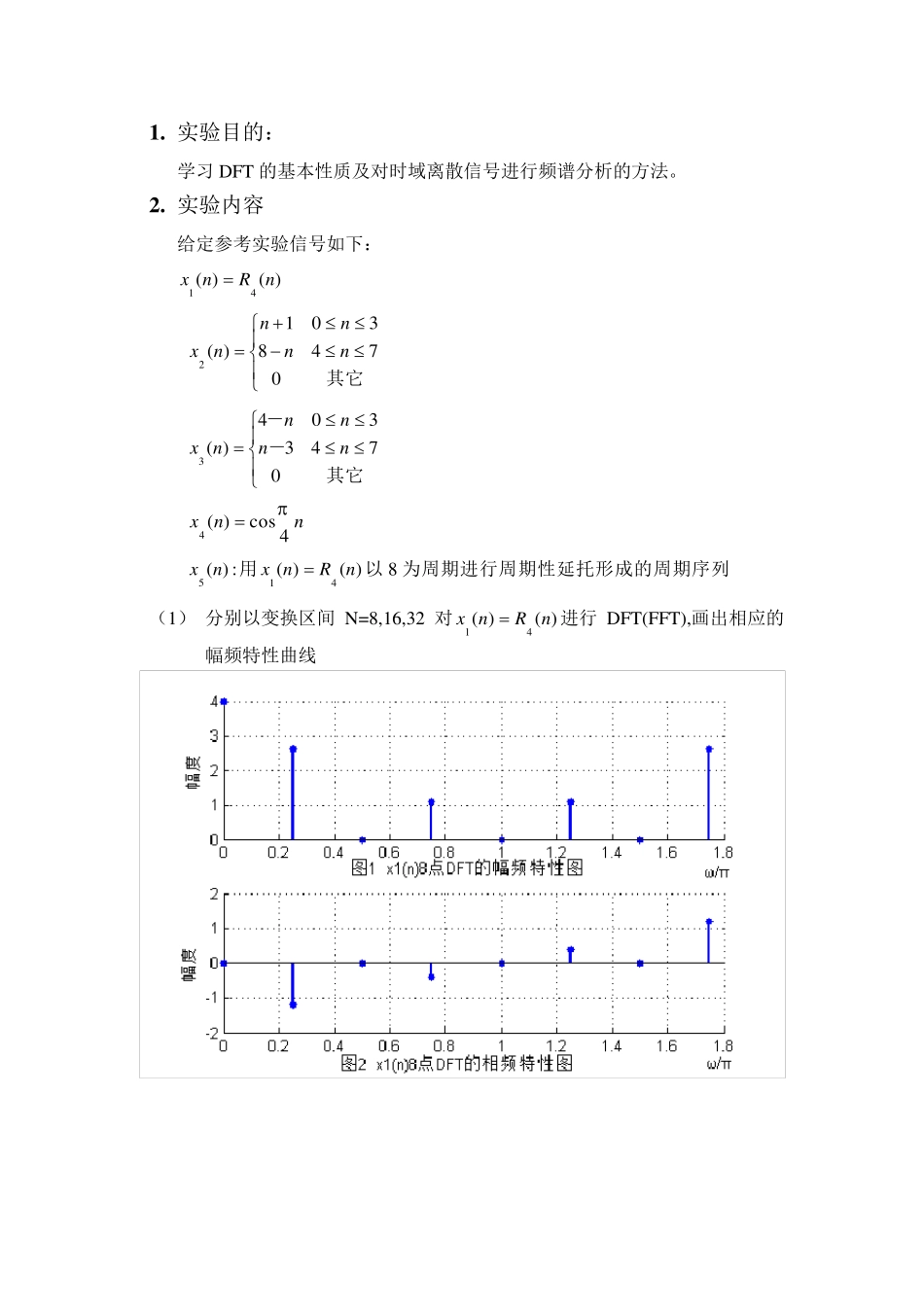
实验报告 用DFT(FFT)对时域离散信号进行频谱分析 1 . 实验目的: 学习DFT 的基本性质及对时域离散信号进行频谱分析的方法。 2 . 实验内容 给定参考实验信号如下: )()(41nRnx 其它0748301)(2nnnnnx 其它--0743304)(3nnnnnx nnx4cos)(4 :)(5 nx用)()(41nRnx以 8 为周期进行周期性延托形成的周期序列 (1) 分别以变换区间 N=8,16,32 对)()(41nRnx进行DFT(FFT),画出相应的幅频特性曲线 (2) 分别以变换区间N=8,16 对)( ),(32nxnx分别进行DFT(FFT), 画出相应的幅频特性曲线。 (3) 分别以变换区间 N=4,8,16 对)(4 nx分别进行 DFT(FFT),画出相应的幅频特性曲线 (4 ) 对)(5 nx进行频谱分析, 请自己选择变换区间,要求画出幅频特性曲线 3 .实验报告: (1)分析讨论: a. 用实验内容中的(1)分析DFT 的变换区间对频域分析的作用,并说明DFT的物理意义。 答:傅里叶变换就是在以时间为自变量的“信号”与以频率为自变量的“频谱”函数之间的某种变换关系。对于有限长序列x(n)的N 点DFT,相当于对 X(ejw)在(0~2π)区间上的N 点等间隔采样;对有限长序列x(n)的N 点DFT,相当于是对X(z)在单位圆上 N 点等间隔采样。DFT 变换区间长度N不同,变换结果 X(k)不同,当N确定后,X(k)与x(n)是一一对应的,当N足够大时,│X(k)│的包络可以逼近曲线,这在进行频谱分析时很重要。 b. 对于试验内容(2),分析当N=8 时,两个信号的幅频特性为什么一样,而N=16 时又不一样。 答:因为3288( )((3))( )x nxnR n,根据 DFT 的隐含周期性,两个函数以N=8 的周期延拓序列相同,且满足循环移位关系,因此此时二者幅频特性相同;当N=16 时,在周期延拓不足的地方补0,并且不满足循环移位关系,因而 ,当N=16 时幅频特性不同。 c. 对于实验内容(3),)(4 nx是一个周期信号,画出它的理论幅度频谱特性。对照理论结果分析该周期信号的变换区间应该如何选取。如果周期信号的周期预先不知道,如何用DFT 分析它的频谱。 答:理论幅度频谱如下: 1)变换区间的选择:对于非周期信号,假设频谱分辨率F,而频谱分辨率直接和FFT 的变换区间有关,因为FFT 能够实现 的频率分辨率是2π/N 因此有最 小 的N>2π/F,根据此式 可以选择FFT 的变换区间;对于周期信号,周期信号的频谱是离 散 谱,只 有用整 数倍 周期的长度作FF...