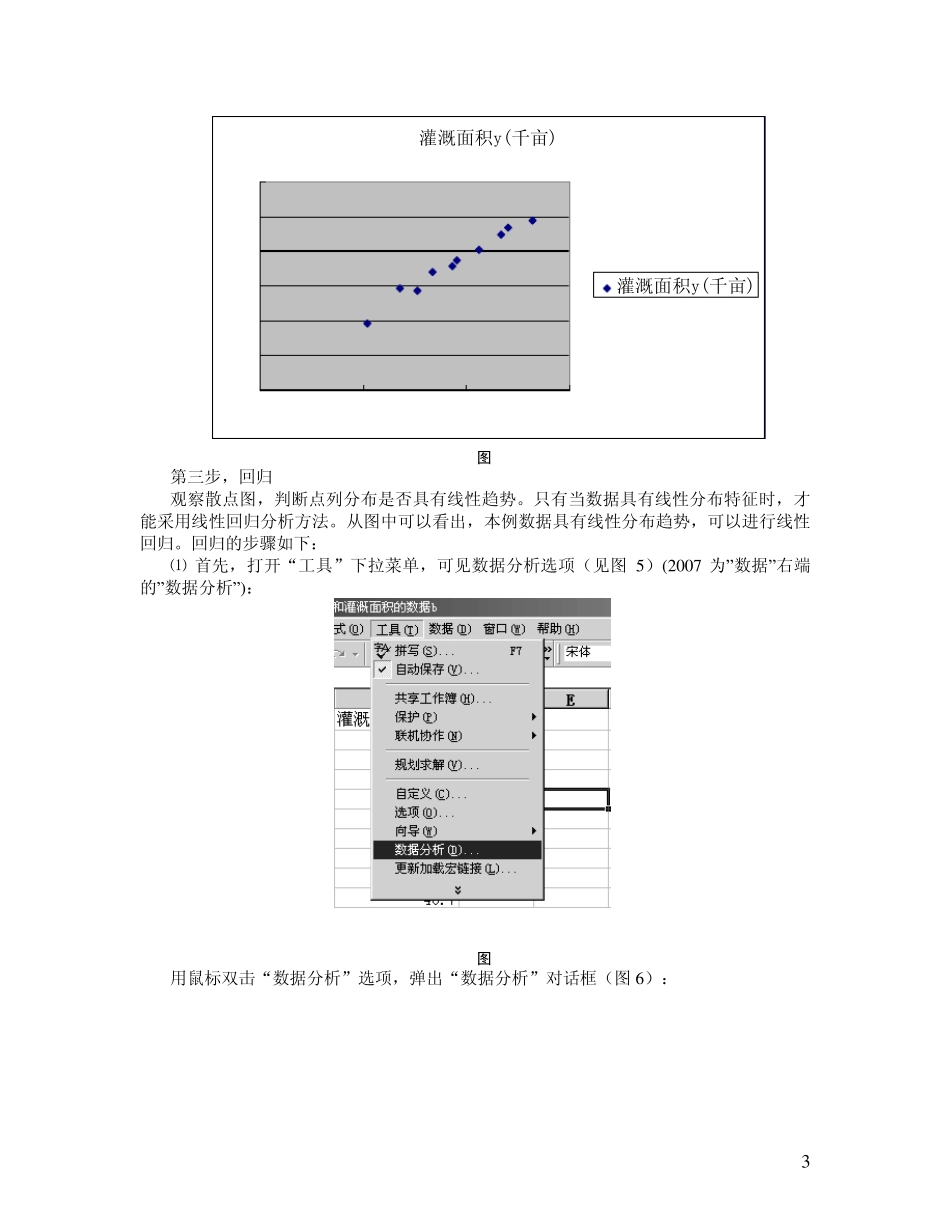
1 用 Ex cel 进行一元线性回归分析 Ex cel 功能强大,利用它的分析工具和函数,可以进行各种试验数据的多元线性回归分析。本文就从最简单的一元线性回归入手. 在数据分析中,对于成对成组数据的拟合是经常遇到的,涉及到的任务有线性描述,趋势预测和残差分析等等。很多专业读者遇见此类问题时往往寻求专业软件,比如在化工中经常用到的 Origin 和数学中常见的 MATLAB 等等。它们虽很专业,但其实使用 Ex cel 就完全够用了。我们已经知道在 Ex cel 自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类数据进行处理。 文章使用的是 2000 版的软件,我在其中的一些步骤也添加了 2007 版的注解. 1 利用 Ex cel2000 进行一元线性回归分析 首先录入数据. 以连续10 年最大积雪深度和灌溉面积关系数据为例予以说明。录入结果见下图(图1)。 图 1 第二步,作散点图 如图2 所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)(ex cel2007)”。图表向导的图标为。选中数据后,数据变为蓝色(图2)。 2 图 2 点击“图表向导”以后,弹出如下对话框(图 3): 图 3 在左边一栏中选中“X Y 散点图”,点击“完成”按钮,立即出现散点图的原始形式(图 4): 3 灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩) 图 4 第三步,回归 观察散点图,判断点列分布是否具有线性趋势。只有当数据具有线性分布特征时,才能采用线性回归分析方法。从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。回归的步骤如下: ⑴ 首先,打开“工具”下拉菜单,可见数据分析选项(见图5 )(2 0 0 7 为”数据”右端的”数据分析”): 图 5 用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6 ): 4 图 6 ⑵ 然后,选择“回归”,确定,弹出如下选项表: 图 7 进行如下选择:X、Y 值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图。 或者:X、Y 值的输入区域(B2:B11,C2:C11),置信度(95%), 新工作表组,残差,线性拟合图。 注意:选中数据“标志”和不选“标志”,X、Y 值的输入区域是不一样的:前者包括数据标志: 最大积雪深度 x(米) 灌溉面积 y(千亩) 后者不包括。这一点务请注意。 5 图8-1 包括数据“标志” 图8-2 不包...