用坐标系解立体几何常见方法

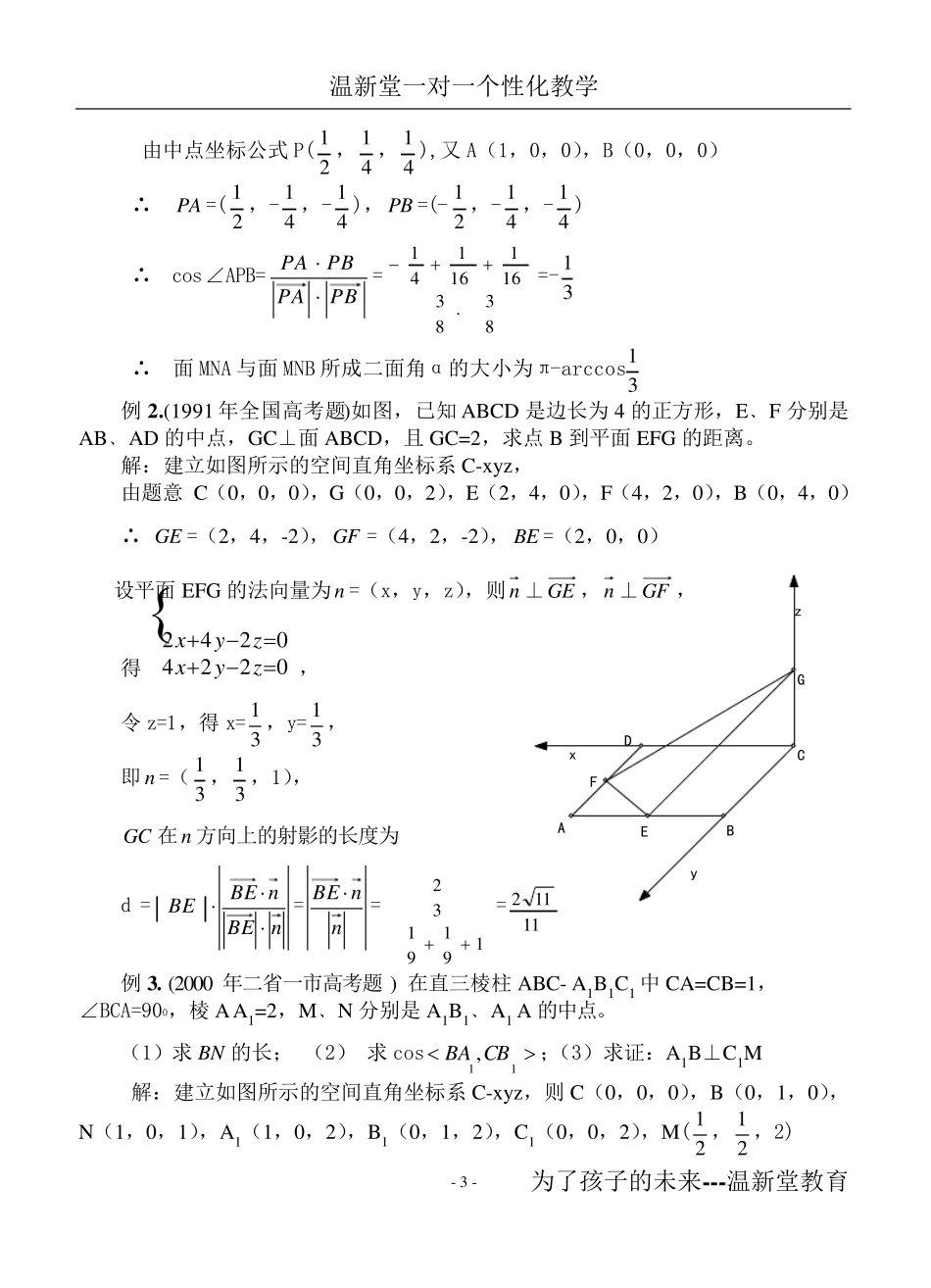
温新堂一对一个性化教学 为了孩子的未来---温新堂教育 - 1 - 建立空间直角坐标系，解立体几何高考题 立体几何重点、热点： 求线段的长度、求点到平面的距离、求直线与平面所成的夹角、求两异面直线的夹角、求二面角、证明平行关系和垂直关系等． 常用公式： 1、求线段的长度：222zyxABAB212212212zzyyxx 2、求P 点到平面 的距离：||||nnPMPN，（N 为垂足，M 为斜足，n 为平面 的法向量） 3、求直线l 与平面 所成的角：|||||||sin|nPMnPM，(lPM ,M, n 为 的法向量) 4、求两异面直线AB 与CD 的夹角：||||||cosCDABCDAB 5、求二面角的平面角 ：|||||||cos|2121nnnn，（ 1n ，2n 为二面角的两个面的法向量） 6、求二面角的平面角 ：SS射影cos，（射影面积法） 7、求法向量：①找；②求：设ba, 为平面 内的任意两个向量，)1,,(yxn 为 的法向量， 则由方程组00nbna，可求得法向量n ． 温新堂一对一个性化教学 为了孩子的未来---温新堂教育 - 2 - 高中新教材9(B)引入了空间向量坐标运算这一内容，使得空间立体几何的平行﹑垂直﹑角﹑距离等问题避免了传统方法中进行大量繁琐的定性分析，只需建立空间直角坐标系进行定量分析，使问题得到了大大的简化。而用向量坐标运算的关键是建立一个适当的空间直角坐标系。 一﹑直接建系。 当图形中有互相垂直且相交于一点的三条直线时，可以利用这三条直线直接建系。 例1 . (2002 年全国高考题)如图，正方形ABCD﹑ABEF 的边长都是1，而且平面ABCD﹑ABEF 互相垂直。点M 在AC 上移动，点N 在BF 上移动，若CM=BN=a（20 a）。 （1）求MN 的长； （2）当a 为何值时，MN 的长最小； （3）当MN 最小时，求面MNA 与面MNB 所成二面角α的大小。 解：（1）以B 为坐标原点，分别以BA﹑BE﹑BC 为x﹑y﹑z 轴建立如图所示的空间直角坐标系B-xyz，由 CM=BN=a，M(a22，0，a221),N（a22，a22，0） ∴ MN =(0，a22， 122a) ∴ MN=22)22()122(aa =21)22(2 a（20 a） （2）由（1）MN=21)22(2 a 所以，当a= 22 时，minMN= 22 ， 即 M﹑N 分别移动到AC﹑BF 的中点时，MN 的长最小，最小值为22 。 （3）取 MN 的中点P，连结 AP﹑BP，因为AM=AN，BM=BN， 所以AP⊥MN，BP⊥MN，∠APB 即为二面角α...