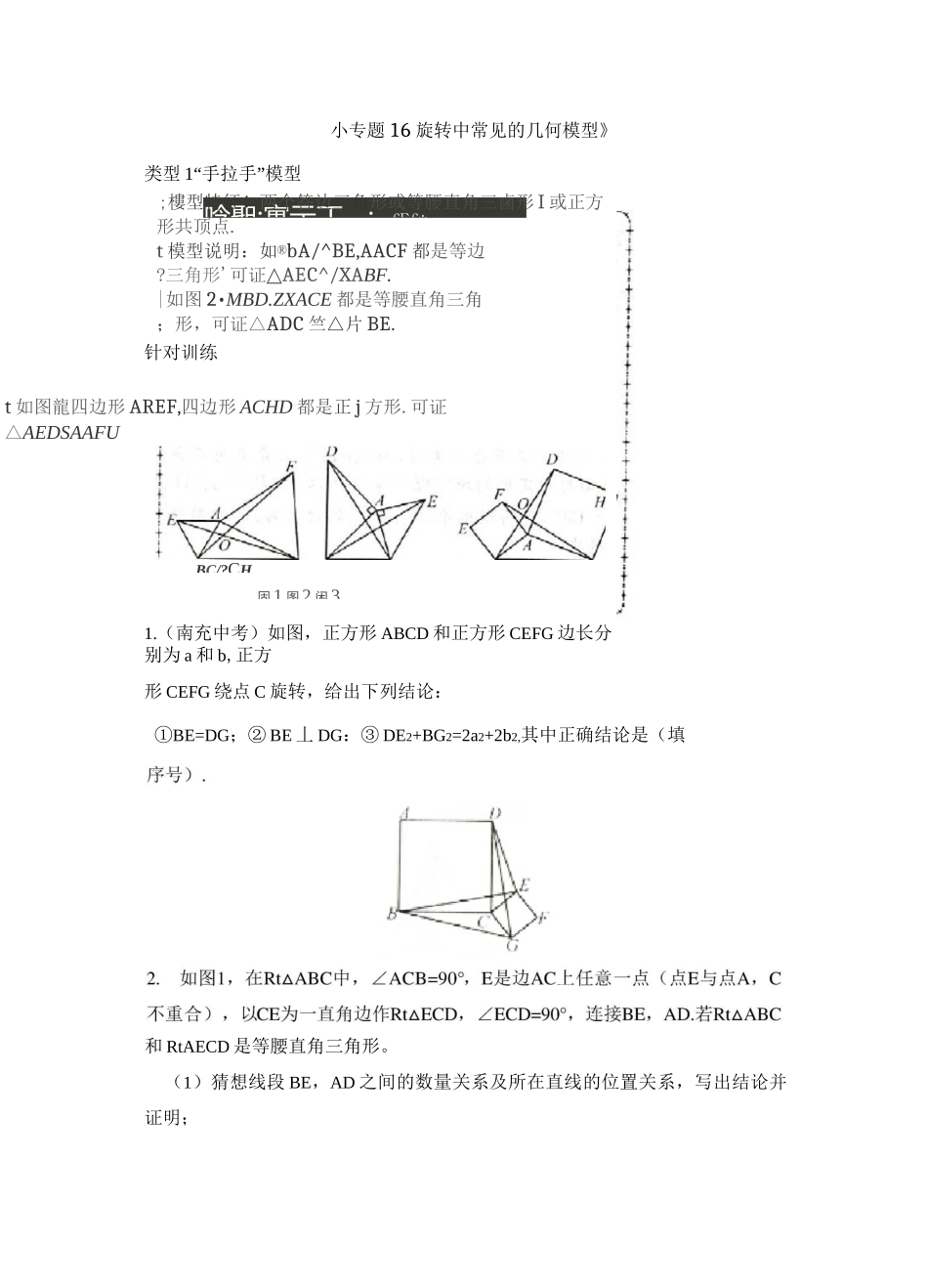
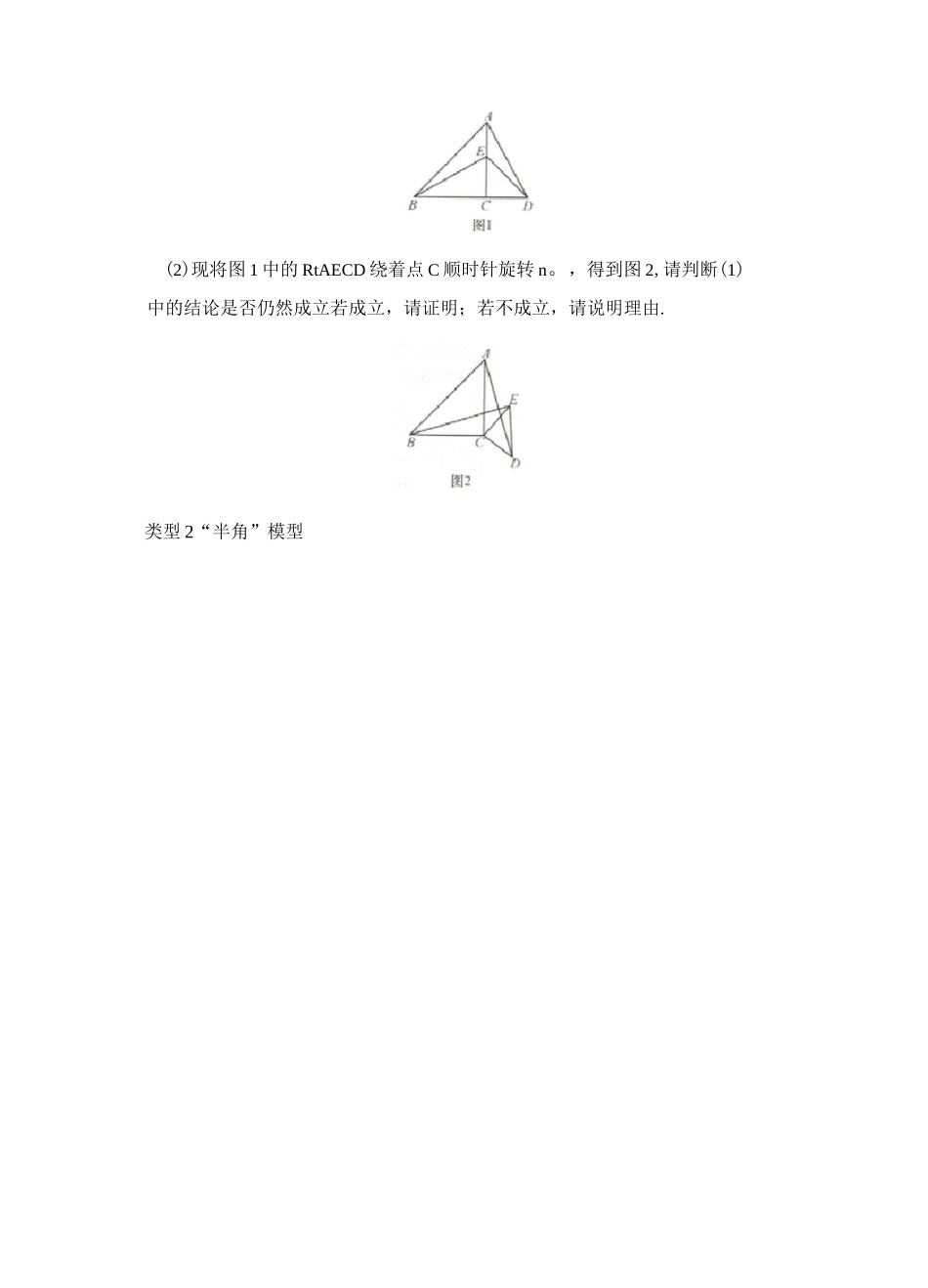
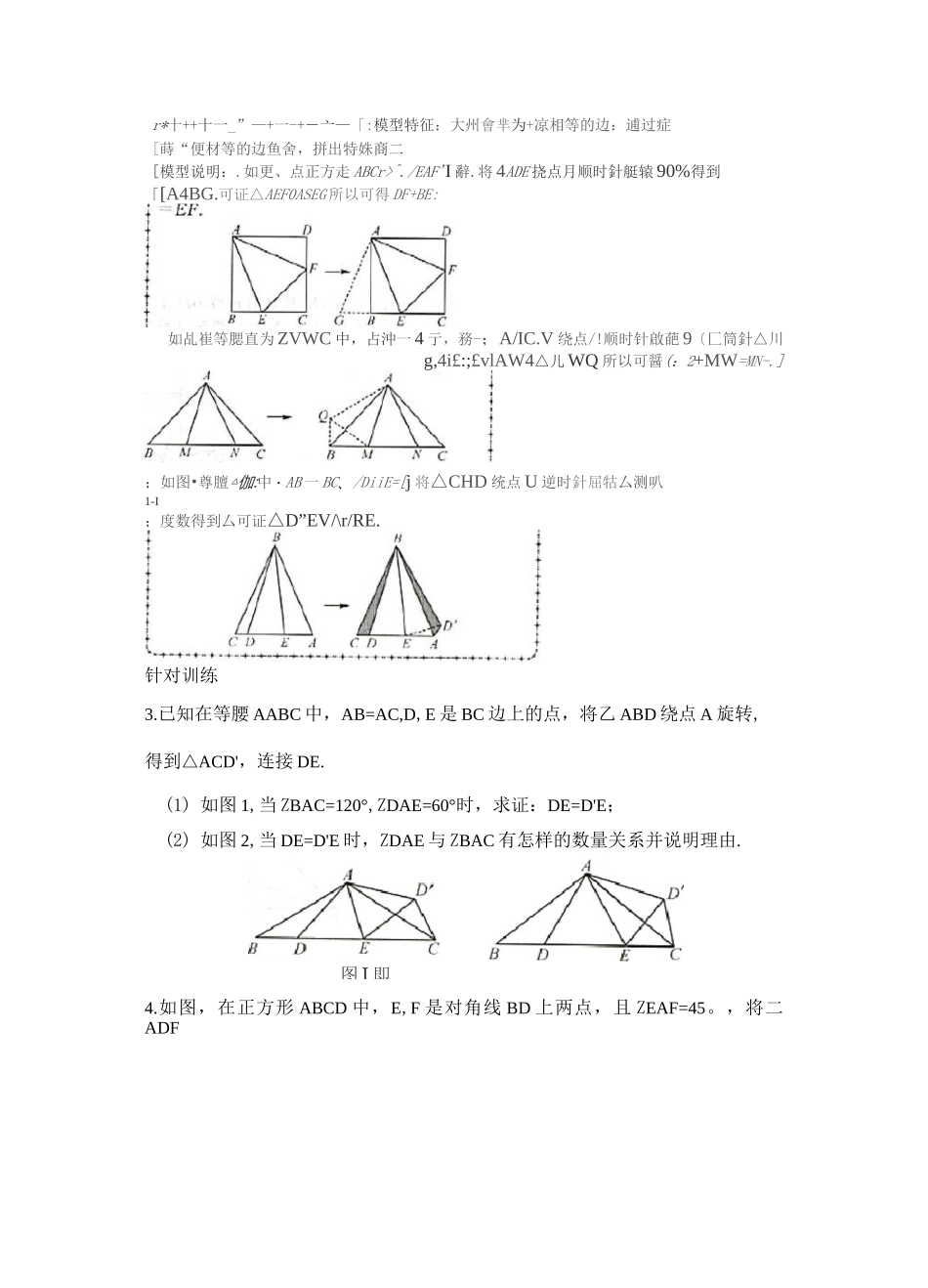
唸聖:寓示丁…:fFf*小专题 16 旋转中常见的几何模型》类型 1“手拉手”模型;樓型特征!两个答边三角形或等腰直角三鹵形 I 或正方形共顶点.t 模型说明:如®bA/^BE,AACF 都是等边?三角形'可证△AEC^/XABF.|如图 2•MBD.ZXACE 都是等腰直角三角;形,可证△ADC 竺△片 BE.针对训练1.(南充中考)如图,正方形 ABCD 和正方形 CEFG 边长分别为 a 和 b,正方形 CEFG 绕点 C 旋转,给出下列结论:t 如图龍四边形 AREF,四边形 ACHD 都是正 j 方形.可证△AEDSAAFUBC/?CH固1 图2 闲3①BE=DG;② BE 丄 DG:③ DE2+BG2=2a2+2b2,其中正确结论是(填和 RtAECD 是等腰直角三角形。(1)猜想线段 BE,AD 之间的数量关系及所在直线的位置关系,写出结论并证明;(2)现将图 1 中的 RtAECD 绕着点 C 顺时针旋转 n。,得到图 2,请判断(1)中的结论是否仍然成立若成立,请证明;若不成立,请说明理由.类型 2“半角”模型图 I 即r*十++十一_”—+一-+―亠—「:模型特征:大州會芈为+凉相等的边:逋过症[蒔“便材等的边鱼舍,拼出特姝商二[模型说明:.如更、点正方走 ABCr>^./EAF'I 辭.将 4ADE 挠点月顺时針艇辕 90%得到「[A4BG.可证△AEF0ASEG 所以可得 DF+BE:如乩崔等腮直为 ZVWC 中,占沖一 4 亍,務-;A/IC.V 绕点/!顺时针啟葩 9〔匚筒針△川g,4i£:;£vlAW4△儿 WQ 所以可醤(:2+MW=MN-.];如图•尊膻△伽:中・AB 一 BC、/DiiE=[j 将△CHD 统点 U 逆时針屈牯厶测叭1-I;度数得到厶可证△D”EV/\r/RE.针对训练3.已知在等腰 AABC 中,AB=AC,D,E 是 BC 边上的点,将乙 ABD 绕点 A 旋转,得到△ACD',连接 DE.(1) 如图 1,当 ZBAC=120°,ZDAE=60°时,求证:DE=D'E;(2) 如图 2,当 DE=D'E 时,ZDAE 与 ZBAC 有怎样的数量关系并说明理由.4.如图,在正方形 ABCD 中,E,F 是对角线 BD 上两点,且 ZEAF=45。,将二ADF绕点 A 顺时针旋转 90°后,得到乙 ABQ,连接 EQ,求证:(1)EA 是 ZQED 的平分线;2)EF2=BE2+DF2.拓展类型构造旋转模型解题厂…-"•—*-*・、・'—•・」-4-士亠-亠一,1 若一半阳晤中舍宵话冃奪的毂極用詩尿的弟鹰.]:退宵是驭答輿总也殳共摆点为雄曲曲密避看浪媾*1[绝脚相善閤捡业沓.脅出奇閱叩国齬.ff■■a 亠!-*一_I-―r4・杠-**”■■+-g1 整■弋 ji|寸円〒.■.討5.【注重阅读理解】请阅读下列材料:问题:如图 1,在等边二 ABC 内有一点 P...