电工基础第3章考题

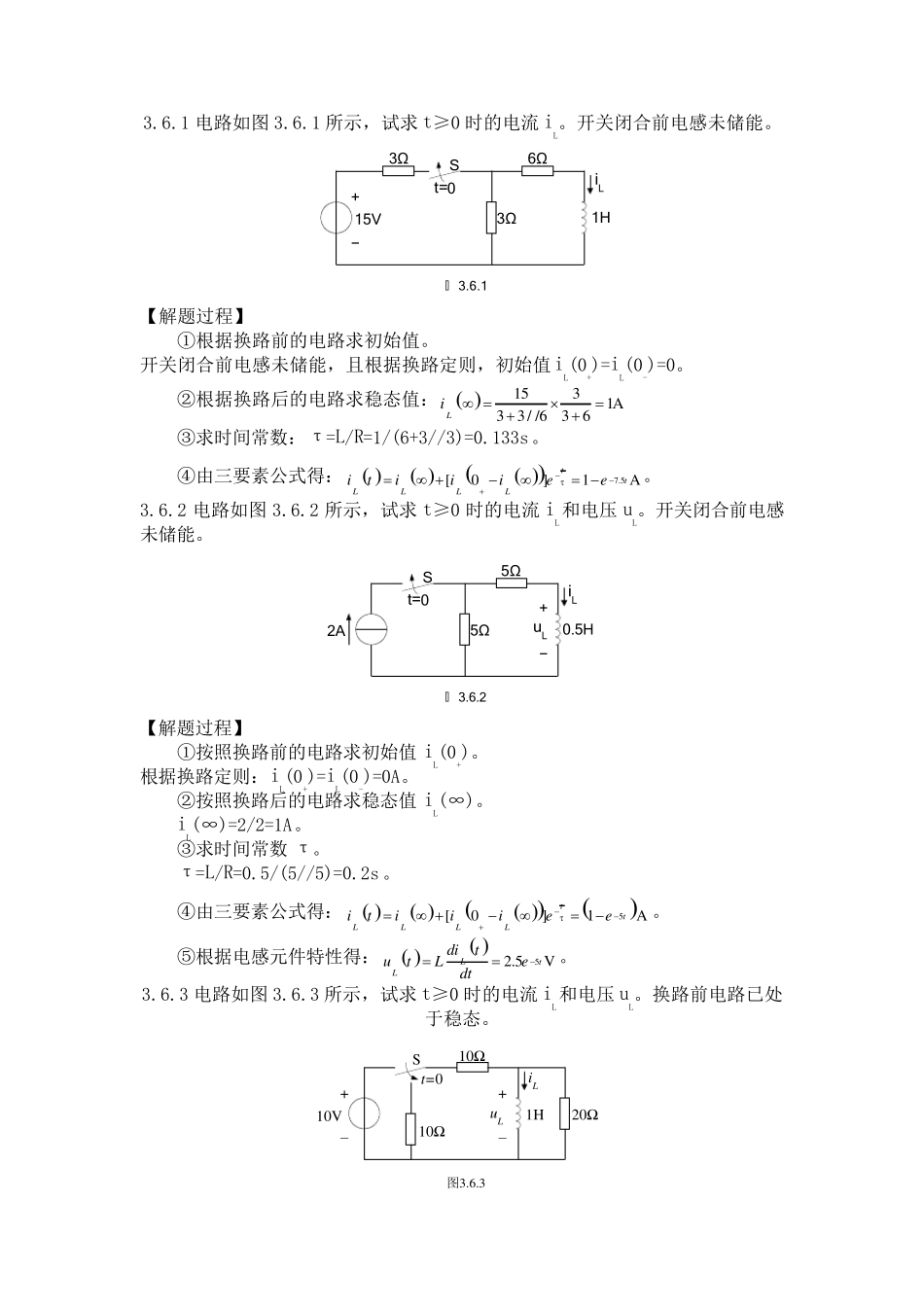
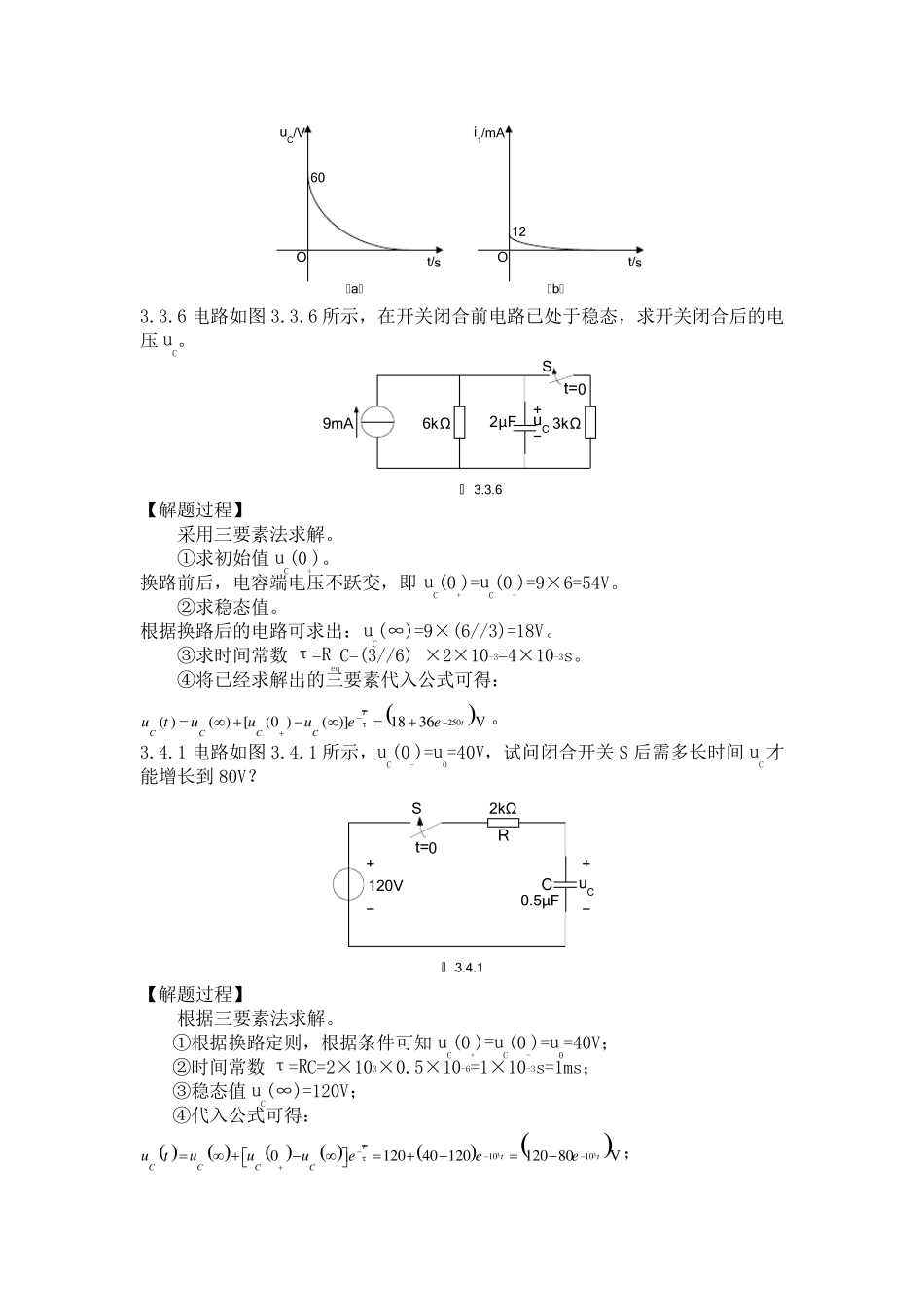
3.6.1 电路如图3.6.1 所示，试求t≥0 时的电流iL。开关闭合前电感未储能。3ΩSt=0iL图 3.6.115V+−6Ω3Ω1H 【解题过程】 ①根据换路前的电路求初始值。 开关闭合前电感未储能，且根据换路定则，初始值iL(0+)=iL(0-)=0。 ②根据换路后的电路求稳态值： 1531A33/ /636Li  ③求时间常数：τ=L/R=1/(6+3//3)=0.133s。 ④由三要素公式得：   7.5[0]1AttLLLLitiiiee  。 3.6.2 电路如图3.6.2 所示，试求t≥0 时的电流iL和电压 uL。开关闭合前电感未储能。 St=0iL图 3.6.22A5Ω5Ω0.5H+−uL 【解题过程】 ①按照换路前的电路求初始值iL(0+)。 根据换路定则：iL(0+)=iL(0-)=0A。 ②按照换路后的电路求稳态值iL(∞)。 iL(∞)=2/2=1A。 ③求时间常数τ。 τ=L/R=0.5/(5//5)=0.2s 。 ④由三要素公式得：   5[0]1AttLLLLitiiiee 。 ⑤根据电感元件特性得：  52.5VLtLditutLedt。 3.6.3 电路如图3.6.3 所示，试求t≥0 时的电流iL和电压 uL。换路前电路已处于稳态。 St=0iL图3.6.310V+−10Ω10Ω1H+−u L20Ω 【解题过程】 ①根据换路前的电路求初始值iL(0+)。 根据换路定则iL(0+)=iL(0-)=10/10=1A。 ②根据换路后的电路求稳态值iL(∞)。 iL(∞)=0A。 ③求时间常数τ。 τ=L/R=1/[(10+10)//20]=0.1s。 ④由三要素公式得：   10[0]AttLLLLitiiiee 。 ⑤由电感元件特性得：  1010VLtLditutLedt 。 3.3.5 在图3.3.5 中，I=10mA，R1=3kΩ，R2=3kΩ，R3=6kΩ，C=2μF。在开关 S 闭合前电路已处于稳态。求在t≥0 时的uC和 i1，并作出它们随时间的变化曲线。 IR2R3R1C+−uCSt=0i1图 3.3.5 【解题过程】 三要素法进行计算。 ①求初始值uC(0+)。 根据换路定则，uC(0+)= uC(0-)= IR3=60V。 ②求时间常数，将电源置零后，电容两端的等效电阻 Req=R1+R2//R3=5kΩ，时间常数τ=ReqC=0.01s 。 R2R3R1Req ③稳态值，由原电路图，因为开关 S 闭合后，电流源被短路，因此电容端电压稳态值为 uC(0+)= uC(∞)= 0V。 ④将三要素代入公式可得：1000.016060VttCuee。直接对之求微分可得100112m AtCduiCedt 。 ⑤确定i1和 uC的起点和终点，即可画出其变化曲线如下： 60uC/Vt/sO(a)12i1/mAt/sO(...