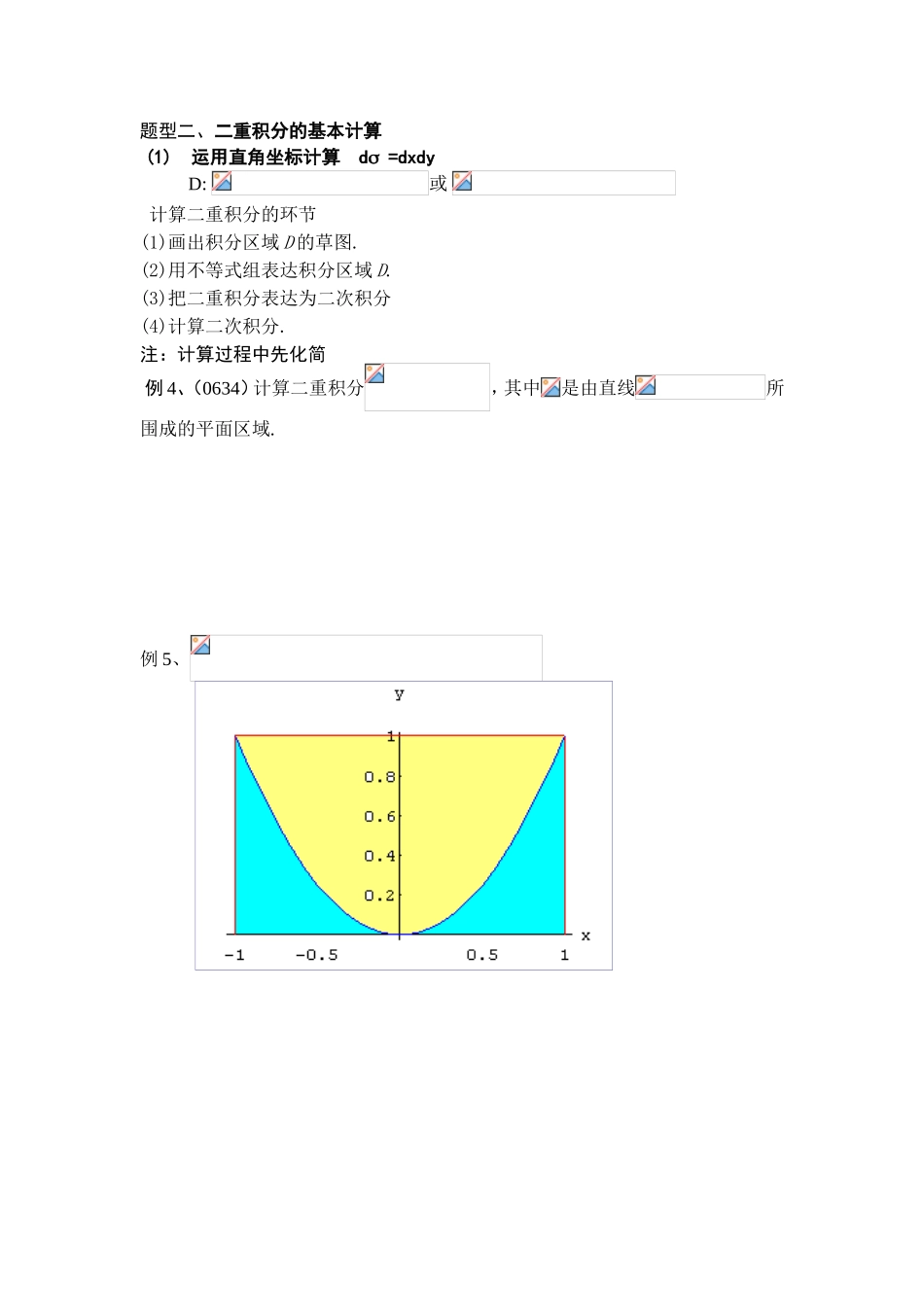
第九讲 二重积分一、考试规定1、理解(理解)二重积分的概念,理解二重积分的基本性质。2、掌握二重积分(直角坐标、极坐标)的计算措施。3、会计算无界区域上的较简单的二重积分(数三、四)二、 内容提要 1、 定义 2、 性质 1) 线性运算性质 2) 积分可加性: 3)假如在 D 上 f(x y)g(x y) 则4)设 M、m 分别是 f(x y)在闭区域 D 上的最大值和最小值 为 D 的面积 则有 5)设函数 f(x y)在闭区域 D 上持续 为 D 的面积 则在 D 上至少存在一点( )使得 3、几何意义 二、重要公式与结论二重积分的对称性质 1) D 有关 x 轴对称 D1为 D 的上半平面。 2) D 有关 y 轴对称 D2为 D 的右半平面。 3) 轮换对称性: 若 x, y 互换后区域 D 不变,则 三、经典题型与例题题型一、基本概念及性质例 1、设闭区域 f(x,y)为 D 上的持续函数,且 求 f(x,y).例 2、(0534)设,,,其中,则(A) (B).(C) . (D) . 例 3、(10123)(A) . (B).(C) . (D). 【 】【答案】 应选(D).【分析】 用二重积分(或定积分)的定义.【详解】 由于 ,因此应选(D).题型二、二重积分的基本计算 (1) 运用直角坐标计算 d =dxdy D: 或 计算二重积分的环节(1)画出积分区域 D 的草图.(2)用不等式组表达积分区域 D. (3)把二重积分表达为二次积分(4)计算二次积分.注:计算过程中先化简 例 4、(0634)计算二重积分,其中是由直线所围成的平面区域.例 5、(2)运用极坐标计算 d =rdrd计算措施同直角坐标,一般先 、后,适应于圆形区域或被积函数具有的因子;(i)极点在区域内: (ii)极点在区域外: (iii)极点在区域的边界上:例 6、(0612)设区域, 计算二重积分例 7、计算,其 D 为由圆,及直线, 所围成的平面闭区域. 计算重积分应注意的技巧:运用重积分的对称性简化计算例 8、计算,例 9、计算= 例 10、 计算, 其中 D:例 11、求,其中 D 是由圆和所围成的平面区域..例 12、计算 I=, D: 例 13、(运用对称性证明不等式) 设 f(x)在[a,b]上持续,且 f(x)>0. 证明: 题型三、几类特殊重积分的计算1、分片函数的重积分例 14、设求例 15、设,表达不超过 的最大整数. 计算二重积分2、 具有绝对值的情形例 16、(05234)计算二重积分,其中.例 17、 计算,其中 3、 互换积分次序的情形例 18、计算...