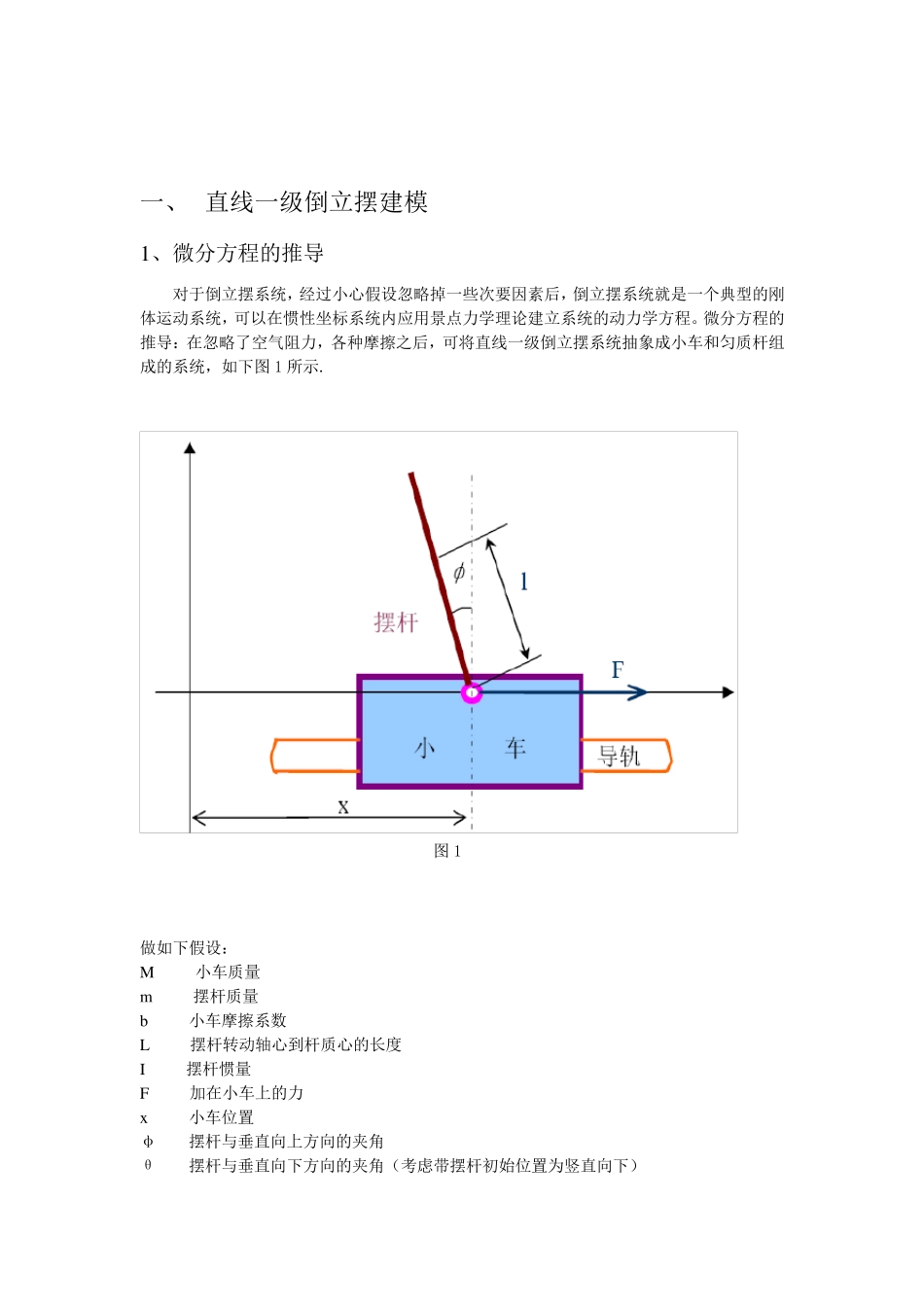
一、 直线一级倒立摆建模 1、微分方程的推导 对于倒立摆系统,经过小心假设忽略掉一些次要因素后,倒立摆系统就是一个典型的刚体运动系统,可以在惯性坐标系统内应用景点力学理论建立系统的动力学方程。微分方程的推导:在忽略了空气阻力,各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如下图1 所示. 图1 做如下假设: M 小车质量 m 摆杆质量 b 小车摩擦系数 L 摆杆转动轴心到杆质心的长度 I 摆杆惯量 F 加在小车上的力 x 小车位置 φ 摆杆与垂直向上方向的夹角 θ 摆杆与垂直向下方向的夹角(考虑带摆杆初始位置为竖直向下) 图2 图2 是系统中小车和摆杆的受力分析图。其中,N 和P为小车和摆杆的相互作用力的水平和垂直方向的分量。在实际倒立摆系统中检测和执行装置的正负方向已经完全确定,所以矢量方向定义如图2 所示,图示方向为矢量的正方向。 分析小车水平方向所受合力,可以得到方程: (式1) 由摆杆水平方向的受力进行分析可以得到下面等式: = (式2、式3) 将式3 代入式1 可得系统第一个运动方程: (式4) 为了推出系统第二个运动方程,对摆杆垂直向上的合力进行分析可得方程: = (式5 式6) 力矩平衡方程如下: (式7) 式中: 合并式6、式7 得第二个运动方程: (式8) 设 ( 是摆杆与垂直向上方向之间的夹角),假设 与 1(单位是弧度)相比很小,即 <<1,则可以进行近似处理: 用 u 来代表被控对象的输入力 F,线性化后两个运动方程如下: (式9 ) 对式(3 -9 )进行拉普拉斯变换(推导传递函数时假设初始条件为 0 。): (式1 0 ) 整理后得到传递函数: (式11 ) 其中: 2 、状态空间方程 设系统状态空间方程为: (式1 2 ) 方程组 对解代 数方程,得到解如下: (式1 3 ) 整理后得到系统状态空间方程: (式1 4 ) 3 、实际系统模型 假定系统物理参数设计如下: M 小车质量 1.08Kg m 摆杆质量 0.1Kg b 小车摩擦系数 0.1N/m/sec l 摆杆转动轴心到杆质心的长度 0.3m I 摆杆惯量 0.0027Kg*m*m 将上述参数带入,可以得到以外界作用力作为输入的系统状态方程: ...