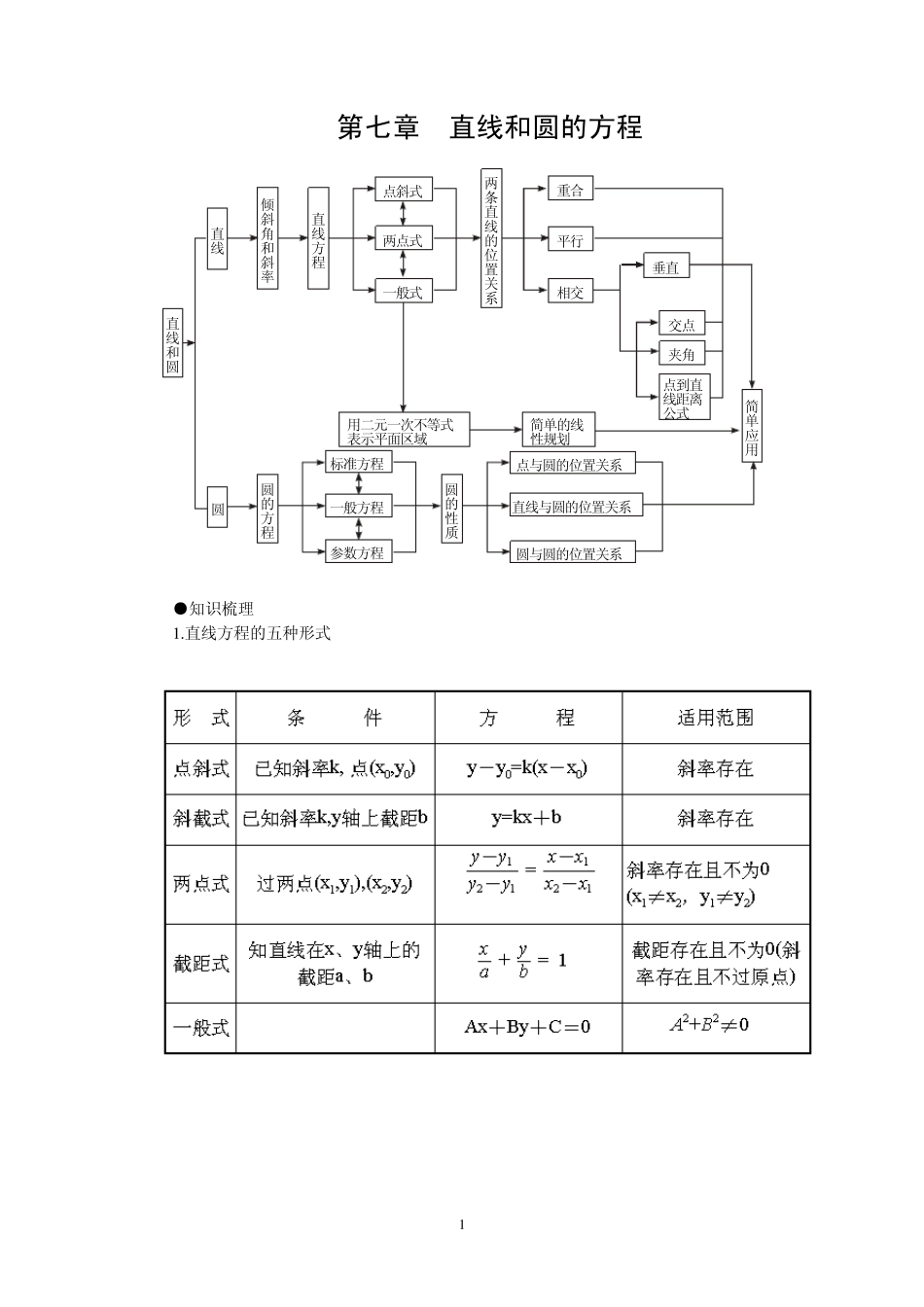
1 第七章 直线和圆的方程 直线和圆直线圆倾斜角和斜率直线方程点斜式两点式一般式两条直线的位置关系重合平行相交垂直交点夹角点到直线距离公式用二元一次不等式表示平面区域简单的线性规划圆的方程标准方程一般方程参数方程圆的性质点与圆的位置关系直线与圆的位置关系圆与圆的位置关系简单应用 ●知识梳理 1 .直线方程的五种形式 2 2.直线的倾斜角、斜率及直线的方向向量及位置关系: (1)直线的倾斜角 在平面直角坐标系中,对于一条与x 轴相交的直线,如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α ,那么α 就叫做直线的倾斜角. 直线和x 轴平行或重合时,直线的倾斜角为0°,直线倾斜角取值范围 0°≤α <180°. (2)直线的斜率 倾斜角α 不是 90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用 k 表示,即k=tanα (α ≠90°). 倾斜角是 90°的直线没有斜率;倾斜角不是 90°的直线都有斜率,其取值范围是(-∞,+∞). (4)求直线斜率的方法 ①定义法:已知直线的倾斜角为α ,且α ≠90°,则斜率k=tanα . ②公式法:已知直线过两点P1(x1,y1)、P2(x2,y2),且 x1≠x2,则斜率k=1212xxyy. 平面直角坐标系内,每一条直线都有倾斜角,但不是每一条直线都有斜率. 对于直线上任意两点P1(x1,y1)、P2(x2,y2),当 x1=x2 时,直线斜率k 不存在,倾斜角α =90°;当 x1≠x2 时,直线斜率存在,是一实数,并且 k≥0 时,α =arctank,k<0 时,α =π +arctank. (5)到角与夹角:若直线l1, l2 的斜率分别为k1, k2,将 l1 绕它们的交点逆时针旋转到与l2 重合所转过的最小正角叫l1 到l2 的角;l1 与l2 所成的角中不超过 900 的正角叫两者的夹角。若记到角为θ ,夹角为α ,则 tanθ =21121kkkk,tanα =21121kkkk. (6)平行与垂直:若直线l1 与l2 的斜率分别为k1, k2。且两者不重合,则 l1//l2 的充要条件是 k1=k2;l1 l2 的充要条件是 k1k2=-1。 (7)两点P1(x1, y1)与P2(x2, y2)间的距离公式:|P1P2|=221221)()(yyxx。 (8)点P(x0, y0)到直线l: Ax+By+C=0 的距离公式:2200||BACByAxd。 3.直线系的方程: 若已知两直线的方程是 l1:A1x+B1y+C1=0 与l2:A2x+B2y+C2=0, 则过 l1, l2 交点的直线方程为A1x+B1y+C1+λ (A2x+B2y+C2)=0; 与l2 平行的直线方程为A1x+B1y...