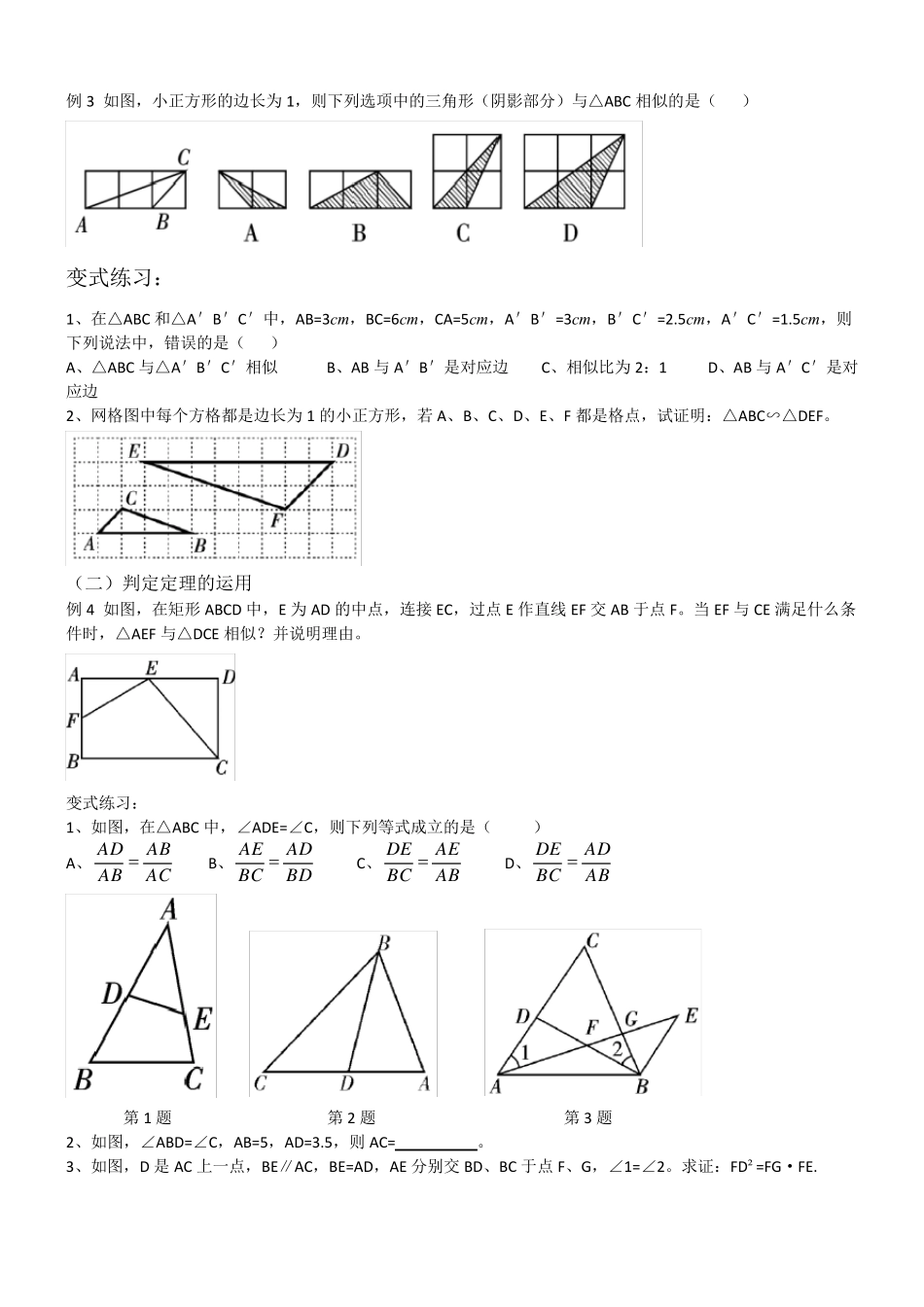
相似三角形的判定 一、知识点讲解 判定定理1:如果一个三角形的两个角与另外一个三角形的两个角对应相等,那么这两个三角形相似。 判定定理2:两边对应相等且夹角对应相等的两个三角形相似。 判定定理3:三边对应成比例的两个三角形相似。 理解:(1)当给出的条件上角为主时,应考虑“两角对应相等”;当给出的条件有边有角时,应考虑“两边对应成比例,夹角相等”;当给出的条件全是边时应考虑“三边对应成比例”。 (2)在利用判定定理2 时,一是两边的夹角相等,如果不是夹角则不成立。 二、典例分析 (一)运用判定定理判定三角形相似 例1 在矩形ABCD 中,E 为BC 上一点,DF⊥AE 于点F。 (1)求证:△ABE∽△DFA;(2)若AB=6,AD=12,AE=10,求DF 的长。 变式练习: 1、如图,DE∥BC,EF∥AB,则图中相似的三角形一共有( ) A、1 对 B、2 对 C、3 对 D、4 对 2、具备下列各组条件的两个三角形中,不一定相似的是( ) A、有一个角是40°两个等腰三角形 B、两个等腰直角三角形 C、有一个角为100°的两个等腰三角形 D、两个等边三角形 例2 已知:如图,在四边形ABCD 中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=217,求AD 的长。 变式练习: 1、如图,在△ABC 中,点D、E 分别在AB、AC 上,下列条件中不能判定△ABC∽△AED 的是( ) A、∠AED=∠B B、∠ADE=∠C C、 ABACAEAD D、 ACAEABAD 2、已知,P是正方形ABCD 的边BC 上的点,且BP=3PC,M 是CD 的中点,求证:△ADM∽△MCP。 例3 如图,小正方形的边长为1,则下列选项中的三角形(阴影部分)与△ABC 相似的是( ) 变式练习: 1、在△ABC 和△A'B'C'中,AB=3cm ,BC=6cm ,CA=5cm ,A'B'=3cm ,B'C'=2.5cm ,A'C'=1.5cm ,则下列说法中,错误的是( ) A、△ABC 与△A'B'C'相似 B、AB 与A'B'是对应边 C、相似比为2:1 D、AB 与A'C'是对应边 2、网格图中每个方格都是边长为1 的小正方形,若A、B、C、D、E、F 都是格点,试证明:△ABC∽△DEF。 (二)判定定理的运用 例4 如图,在矩形ABCD 中,E 为AD 的中点,连接EC,过点E 作直线EF 交AB 于点F。当EF 与CE 满足什么条件时,△AEF 与△DCE 相似?并说明理由。 变式练习: 1、如图,在△ABC 中,∠ADE=∠C,则下列等式成立的是( ) A、 ACABABAD B、 BDADBCAE C、 ABAEBCDE D、 ABADBCDE 第1 ...