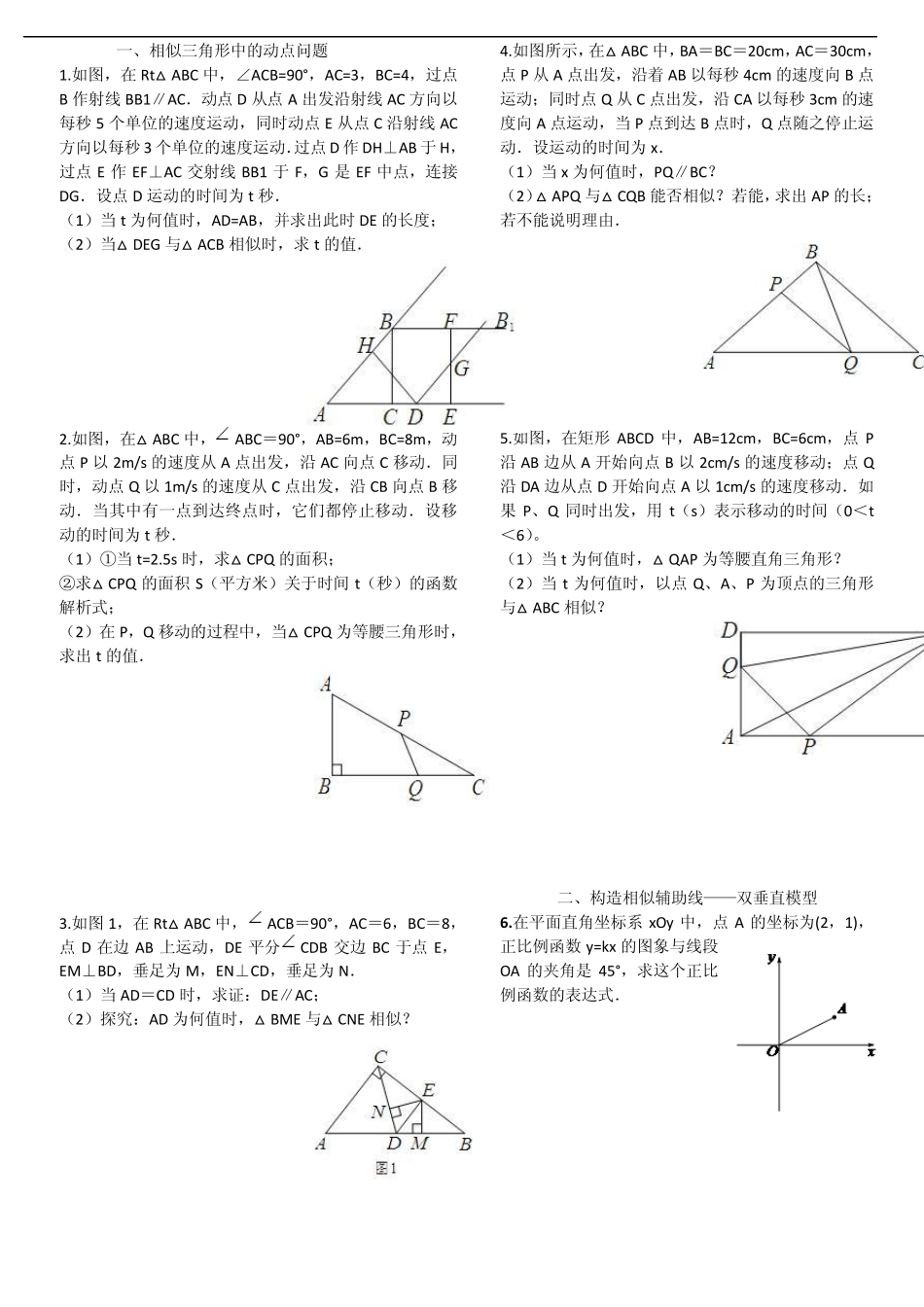
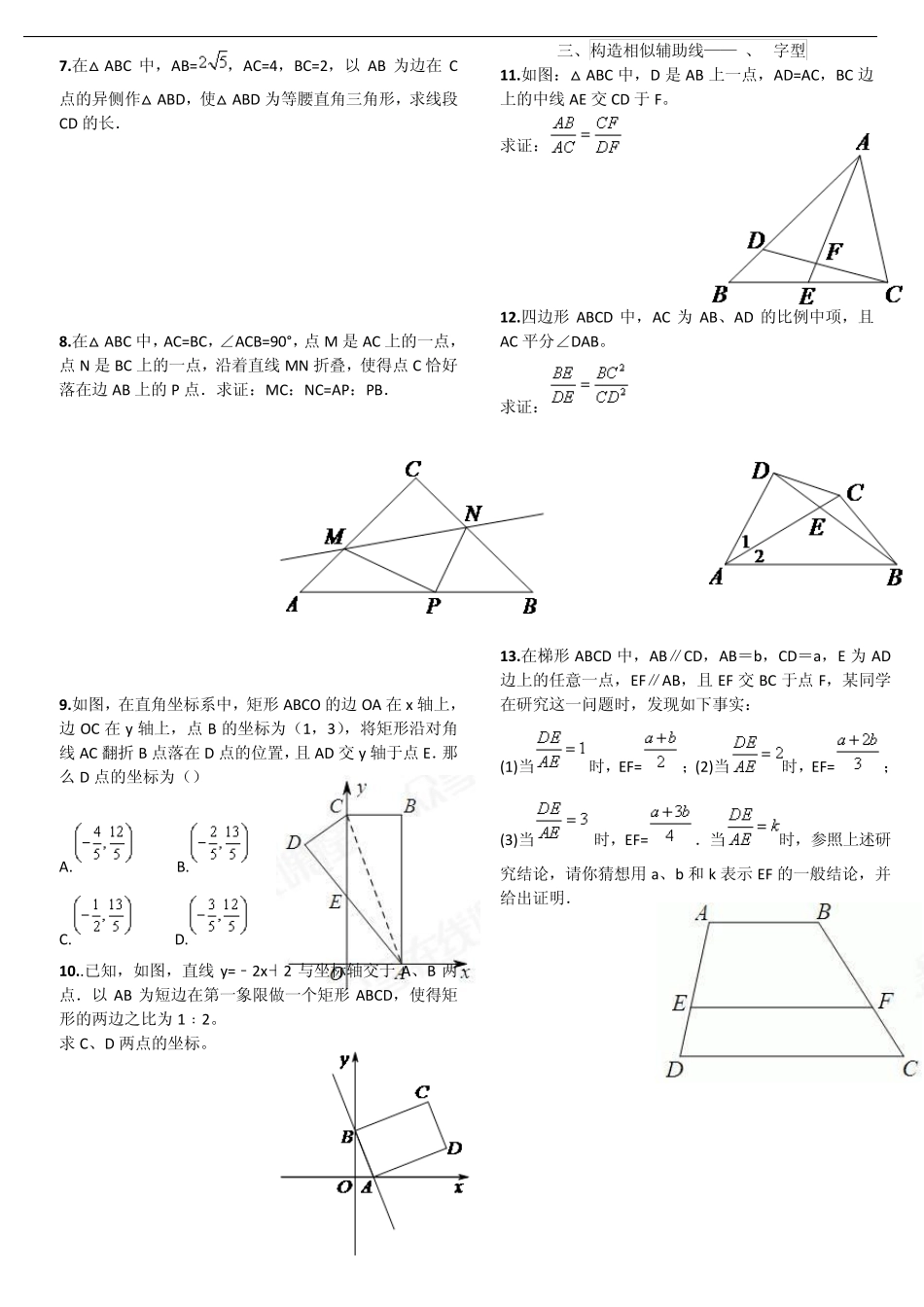
一、相似三角形中的动点问题 1.如图,在Rt△ABC 中,∠ACB=90°,AC=3,BC=4,过点B 作射线BB1∥AC.动点D 从点A 出发沿射线AC 方向以每秒5 个单位的速度运动,同时动点E 从点C 沿射线AC方向以每秒3 个单位的速度运动.过点D 作DH⊥AB 于H,过点E 作EF⊥AC 交射线BB1 于F,G 是EF 中点,连接DG.设点D 运动的时间为t 秒. (1)当t 为何值时,AD=AB,并求出此时DE 的长度; (2)当△DEG 与△ACB 相似时,求t 的值. 2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移动.同时,动点Q 以1m/s 的速度从C 点出发,沿CB 向点B 移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t 秒. (1)①当t=2.5s 时,求△CPQ 的面积; ②求△CPQ 的面积S(平方米)关于时间t(秒)的函数解析式; (2)在P,Q 移动的过程中,当△CPQ 为等腰三角形时,求出t 的值. 3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D 在边AB 上运动,DE 平分CDB 交边BC 于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N. (1)当AD=CD 时,求证:DE∥AC; (2)探究:AD 为何值时,△BME 与△CNE 相似? 4.如图所示,在△ABC 中,BA=BC=20cm,AC=30cm,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,当P 点到达B 点时,Q 点随之停止运动.设运动的时间为x. (1)当x 为何值时,PQ∥BC? (2)△APQ 与△CQB 能否相似?若能,求出AP 的长;若不能说明理由. 5.如图,在矩形ABCD 中,AB=12cm,BC=6cm,点P沿AB 边从A 开始向点B 以2cm/s 的速度移动;点Q沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P、Q 同时出发,用t(s)表示移动的时间(0<t<6)。 (1)当t 为何值时,△QAP 为等腰直角三角形? (2)当t 为何值时,以点Q、A、P 为顶点的三角形与△ABC 相似? 二、构造相似辅助线——双垂直模型 6 .在平面直角坐标系 xOy 中,点A 的坐标为(2,1),正比例函数y=kx 的图象与线段OA 的夹角是45°,求这个正比例函数的表达式. 7.在△ABC 中,AB=,AC=4,BC=2,以AB 为边在C点的异侧作△ABD,使△ABD 为等腰直角三角形,求线段CD 的长. 8.在△ABC 中,AC=BC,∠ACB=90°,点M 是AC 上的一点,点N 是BC 上的一点,沿着直线...