矩阵代数基本知识

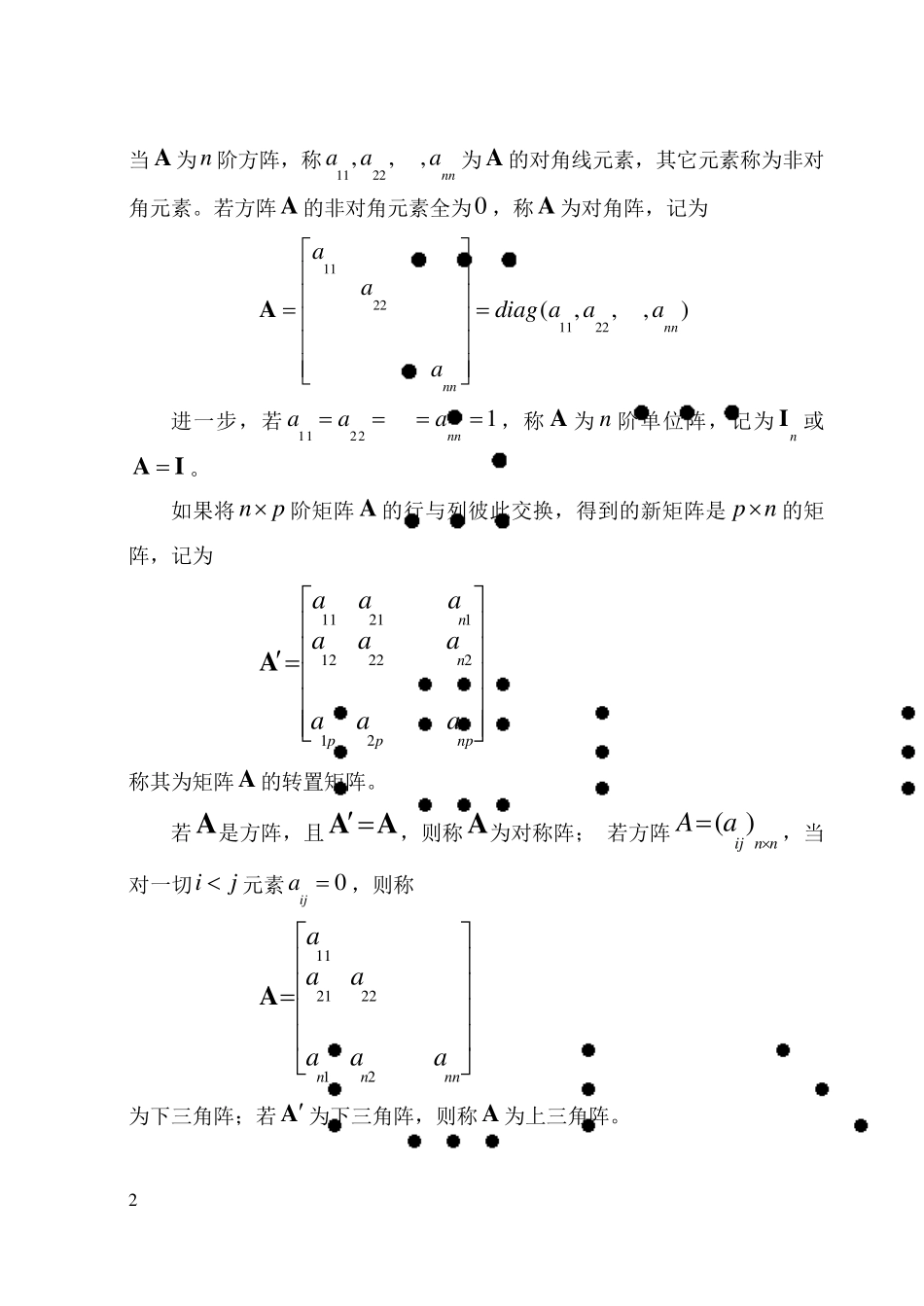
1 附录I 矩阵代数基本知识 矩阵和行列式是研究多元统计分析的重要工具，这里针对本书的需要，对有关矩阵代数的基本知识作回顾性的介绍，其中有些内容是过去教学计划中没有涉及到的。 一、 向量矩阵的定义 将 np个实数1 11 212 12 2212,,,,,,,,,,,,ppnnn paaaaaaaaa排成如下形式的矩形数表，记为A 1 11 212 12 2212ppnnn paaaaaaaaaA 则称A 为 np阶矩阵，一般记为()ijnpaA，称ija 为矩阵A 的元素。当np时，称A 为 n 阶方阵；若1p  ，A 只有一列，称其为n 维列向量，记为 1 12 11naaa 若1n ，A 只有一行，称其为 p 维行向量，记为 1 11 21,,,paaa 2 当A 为n 阶方阵，称1 12 2,,,n naaa为A 的对角线元素，其它元素称为非对角元素。若方阵A 的非对角元素全为0 ，称A 为对角阵，记为 1 12 21 12 2(,,,)n nn naadiag aaaaA 进一步，若1 12 21n naaa，称A 为n 阶单位阵，记为nI 或AI。 如果将 np阶矩阵A 的行与列彼此交换，得到的新矩阵是 pn的矩阵，记为 1 12 111 22 2212nnppn paaaaaaaaaA 称其为矩阵A 的转置矩阵。 若A是方阵，且 AA，则称A为对称阵； 若方阵( )ij n nAa，当对一切ij元素0ija ，则称 1 12 12 212nnn naaaaaaA 为下三角阵；若A 为下三角阵，则称A 为上三角阵。 3 二、 矩阵的运算 1 ．对()ijn paA与()ijn pbB的和定义为： ()ijijn pabAB 2 ．若a 为一常数，它与矩阵np阶矩阵 A 的积定义为： ()ijn paaaA 3 ．若()ikp qaA，()kjq nbB，则 A 与B 的积定义为： 1()qikkjp nka b AB 根据上述矩阵加法、数乘与乘的运算，容易验证下面运算规律： 1 ．加法满足结合律和交换律 ()()ABCABC ABBA 2 ．乘法满足结合律 ()()aaAA ， ()()()aaaABA BAB ()()A BCAB C 3 ．乘法和加法满足分配律 ()aaaABAB， ()aaAAA ()A BCABAC ，()AB CACBC 4 ．对转置运算规律 ()ABAB ， ()()aaAA () ABB A ， ()AA 另外，若()ijn naA满足A AAAI，...