1 第四章 二元关系 例1 设A={0,1},B={a,b},求AB , BA,AA 。 解: AB={<0,a>,<0,b>,<1,a>,<1,b>} BA={
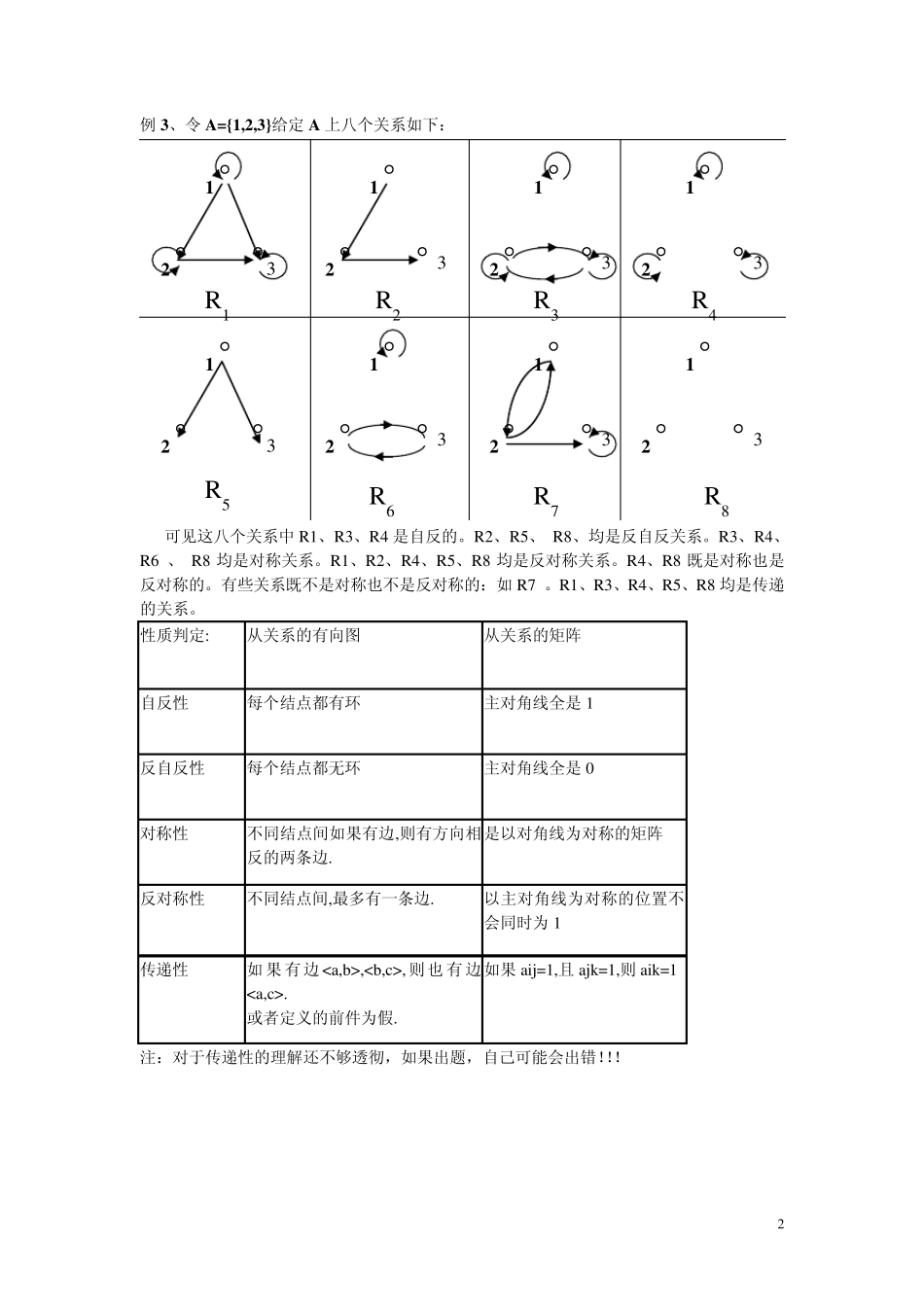
,,,} AA={<0,0>,<0,1>,<1,0>,<1,1>} 可见 A×B≠B×A 例2、关于笛卡尔乘积的几个证明 1)如果 A、B 都是有限集,且|A|=m, |B|=n,则 |AB |=mn. 证明:由笛卡尔积的定义及排列组合中的乘法原理,直接推得此定理。 2) AΦ =Φ B=Φ 3) 对∪和∩满足分配律。 设A,B,C 是任意集合,则 ⑴ A(B∪C)= (AB)∪(AC); ⑵ A(B∩C)= (AB)∩(AC); ⑶ (A∪B)C= (AC)∪(BC); ⑷ (A∩B)C= (AC)∩(BC) 证明 ⑴ :任取A(B∪C) xA yB∪C xA (yB∨yC) ( xA yB)∨(xAyC) AB∨AC (AB)∪(AC) 所以⑴式成立。 4)若 C,,则 AB(ACBC) (CACB). 证明: 必要性:设AB,求证 ACBC 任取AC xAyC xByC (因 AB) BC 所以, ACBC. 充分性: 若 C, 由 ACBC 求证 AB 取 C 中元素 y, 任取 xA xAyCAC BC (由 ACBC ) xByC xB 所以, AB. 所以 AB(ACBC) 类似可以证明 AB (CACB). 5) 设A、B、C、D 为非空集合,则 ABCDAC∧BD. 证明: 首先,由 ABCD 证明 AC∧BD. 任取 xA,任取 yB,所以 xAyB A×B C×D (由 ABCD ) xCyD 所以, AC∧BD. 其次, 由 AC,BD. 证明 ABCD 任取A×B A×B xAyB xCyD (由 AC,BD) C×D 所以, ABCD 证毕. 2 例3、令 A={1,2,3}给定 A 上八个关系如下: 可见这八个关系中 R1、R3、R4 是自反的。R2、R5、 R8、均是反自反关系。R3、R4、 R6 、 R8 均是对称关系。R1、R2、R4、R5、R8 均是反对称关系。R4、R8 既是对称也是反对称的。有些关系既不是对称也不是反对称的:如 R7 。R1、R3、R4、R5、R8 均是传递的关系。 性质判定: 从关系的有向图 从关系的矩阵 自反性 每个结点都有环 主对角线全是 1 反自反性 每个结点都无环 主对角线全是 0...