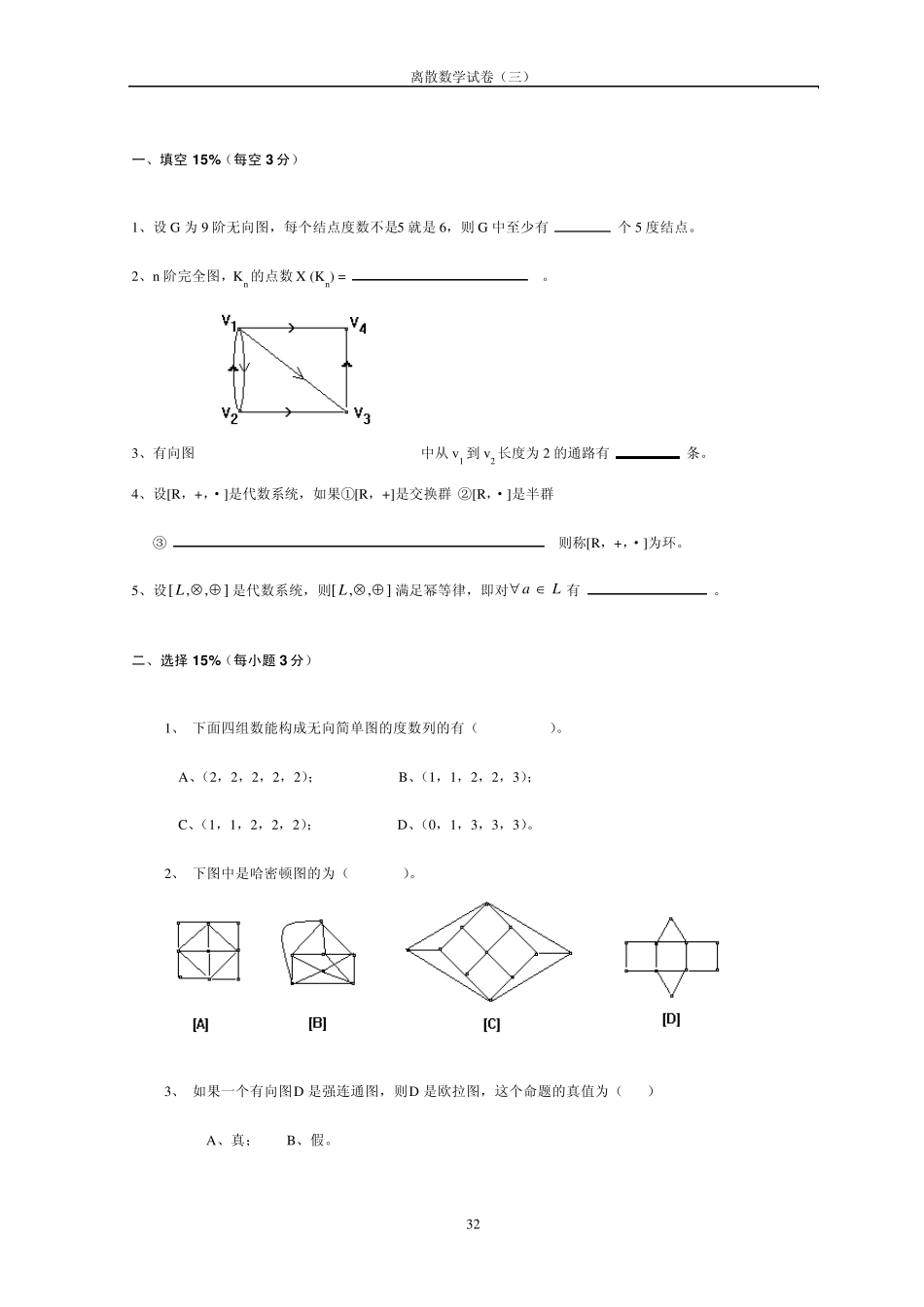
离散数学试卷(三) 32 一、填空 15%(每空 3分) 1、设G 为9 阶无向图,每个结点度数不是5 就是6,则G 中至少有 个5 度结点。 2、n 阶完全图,Kn 的点数X (Kn) = 。 3、有向图 中从v 1 到v 2 长度为2 的通路有 条。 4、设[R,+,·]是代数系统,如果①[R,+]是交换群 ②[R,·]是半群 ③ 则称[R,+,·]为环。 5、设],,[L是代数系统,则],,[L满足幂等律,即对La 有 。 二、选择 15%(每小题 3分) 1、 下面四组数能构成无向简单图的度数列的有( )。 A、(2,2,2,2,2); B、(1,1,2,2,3); C、(1,1,2,2,2); D、(0,1,3,3,3)。 2、 下图中是哈密顿图的为( )。 3、 如果一个有向图D 是强连通图,则D 是欧拉图,这个命题的真值为( ) A、真; B、假。 离散数学试卷(三) 33 4、 下列偏序集( )能构成格。 5、 设}4,41,3,31,2,21,1{s,*为普通乘法,则[S,*]是()。 A、代数系统; B、半群; C、群; D、都不是。 三、证明 48% 1、(10%)在至少有2 个人的人群中,至少有2 个人,他们有相同的朋友数。 2、(8%)若图 G 中恰有两个奇数度顶点,则这两个顶点是连通的。 3、(8%)证明在 6 个结点 12 条边的连通平面简单图中, 每个面的面数都是3。 4、(10%)证明循环群的同态像必是循环群。 5、(12%)设]1,0,,,,[B是布尔代数,定义运算*为)()(*bababa, 求证[B,*]是阿贝尔群。 四、计算 22% 1、在二叉树中 1) 求带权为 2,3,5,7,8 的最优二叉树T。(5 分) 2) 求 T 对应的二元前缀码。(5 分) 2、 下图所示带权图中最优投递路线并求出投递路线长度(邮局在 D 点)。 离散数学试卷(三) 3 4 离散数学试卷(三) 35 一、填空(15%)每空3 分 1、 6;2、n;3、2;4、+对·分配且·对+分配均成立;5、aaaaaa且。 二、选择(15%)每小题 3分 题目 1 2 3 4 5 答案 A,B B,D B C D 三、证明(48%) 1、(10 分)证明:用 n 个顶点 v1,…,vn 表示 n 个人,构成顶点集 V={v1,…,vn} ,设,,,|{v)(uvuVvuuvE是朋友且无向图 G=(V,E) 现证 G 中至少有两个结点度数相同。 事实上,(1)若 G 中孤立点个数大于等于 2,结论成立。 (2) 若 G 中有一个孤立点,则 G 中的至少有 3 个顶点,既不考虑孤立点。设 G 中每...