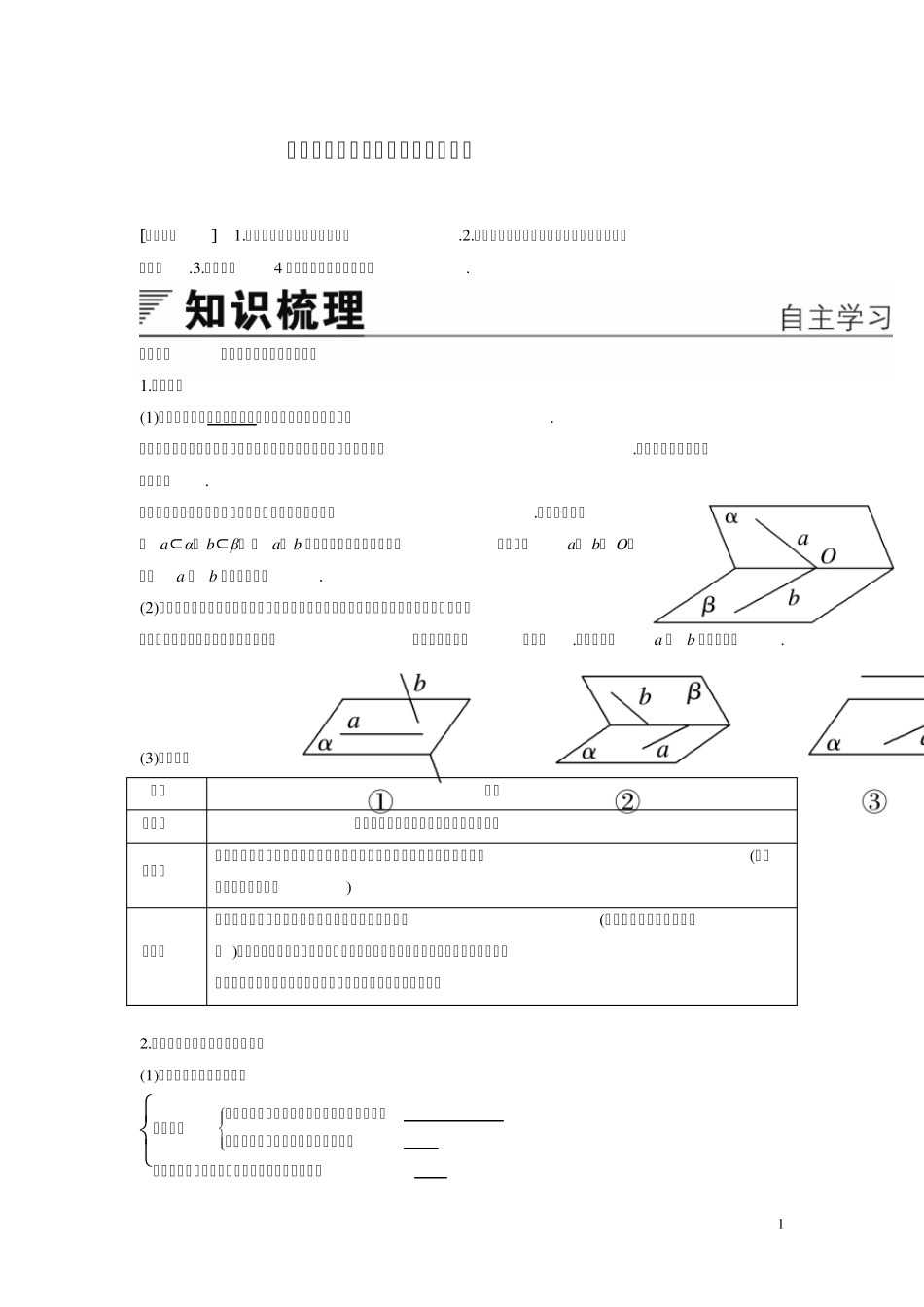
1 空间中直线与直线之间的位置关系 [学习目标] 1 .会判断空间两直线的位置关系.2 .理解两异面直线的定义,会求两异面直线所成的角.3 .能用公理4 解决一些简单的相关问题. 知识点一 空间中两条直线的位置关系 1 .异面直线 (1 )定义:不同在任何一个平面内的两条直线叫做异面直线. 要点分析:①异面直线的定义表明:异面直线不具备确定平面的条件.异面直线既不相交,也不平行. ②不能误认为分别在不同平面内的两条直线为异面直线.如图中,虽然有 a⊂α, b⊂β, 即 a, b分别在两个不同的平面内,但是因为a∩ b= O,所以a与 b不是异面直线. (2 )画法:画异面直线时,为了充分显示出它们既不平行也不相交,即不共面的特点,常常需要画一个或两个辅助平面作为衬托,以加强直观性、立体感.如图所示,a与 b为异面直线. (3 )判断方法 方法 内容 定义法 依据定义判断两直线不可能在同一平面内 定理法 过平面外一点与平面内一点的直线和平面内不经过该点的直线为异面直线(此结论可作为定理使用) 反证法 假设这两条直线不是异面直线,那么它们是共面直线(即假设两条直线相交或平行 ),结合原题中的条件,经正确地推理,得出矛盾,从而判定假设“两条直线不是异面直线”是错误的,进而得出结论:这两条直线是异面直线 2 .空间中两条直线位置关系的分类 (1 )按两条直线是否共面分类 共面直线 相交直线:同一平面内,有且只有一个公共点平行直线:同一平面内,没有公共点异面直线:不同在任何一个平面内,没有公共点 2 (2)按两条直线是否有公共点分类 有且仅有一个公共点——相交直线无公共点 平行直线异面直线 思考 (1)分别在两个平面内的两条直线一定是异面直线吗? (2)两条垂直的直线必相交吗? 答 (1)不一定.可能相交、平行或异面. (2)不一定.可能相交垂直,也可能异面垂直. 知识点二 公理4(平行公理) 文字语言 平行于同一条直线的两条直线互相平行,这一性质叫做空间平行线的传递性 符号语言 a∥ cb∥ c ⇒a∥ b 图形语言 知识点三 空间等角定理 1.定理 文字语言 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 符号语言 OA∥ O′ A′, OB∥ O′ B′ ⇒∠ AOB=∠A′ O′ B′或∠AOB+∠A′ O′ B′= 180° 图形语言 作用 判断或证明两个角相等或互补 2.推广 如果两条相交直线与另两条相交直...