空间向量立体几何(绝对经典)

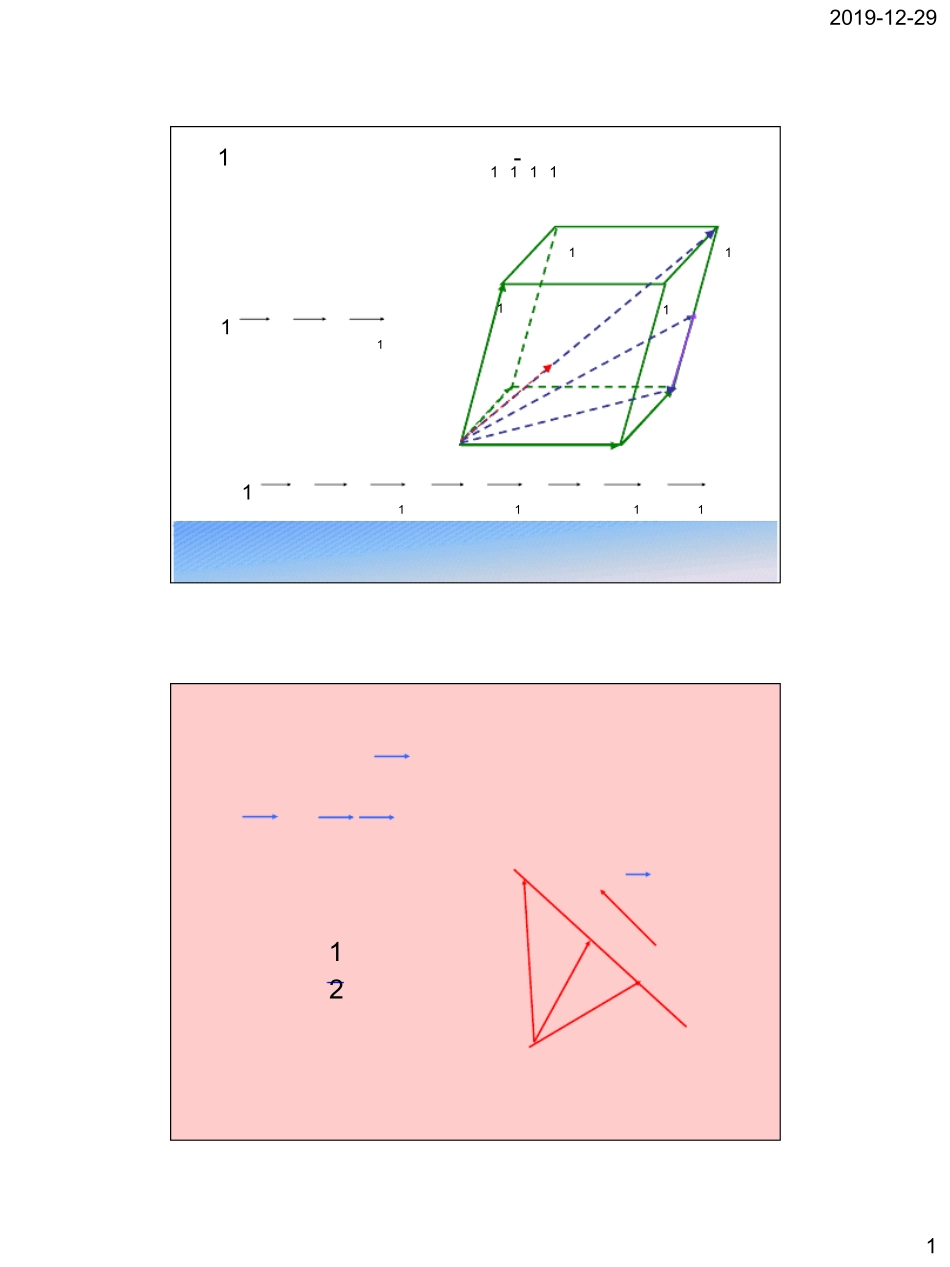
2019-12-291例1：已知平行六面体ABCD-A1B1C1D1，化简下列向量表达式，并标出化简结果的向量。(如图)ABCDA1B1C1D1G1)1(AAADAB1111)1(ACCCACAAACAAADAB解M 始点相同的三个不共面向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量 推论: 如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式OP=OA+t 其中向量叫做直线的方向向量.llaaOABPa 若P为A,B中点, 则12 OPOA OB2019-12-2922.共面向量定理:如果两个向量 不共线,则向量 与向量 共面的充要条件是存在实数对 使,abyx,p,abOM abABAPpp xayb 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使 或对空间任一点O,有 MP xMAyMB OP OM xMAyMB注意：空间四点P、M、A、B共面 存在唯一实数对, ,x yMP xMAyMB（） 使得(1)OP xOM yOAzOBx y z  其中，2019-12-293例1：已知m,n是平面内的两条相交直线，直线l与的交点为B，且l⊥m，l⊥n，求证：l⊥。nmggmnll证明：在内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g，因m与n相交，得向量m、n不平行，由共面向量定理可知，存在唯一的有序实数对（x，y），使 g=xm+yn, l·g=xl·m+yl·n l·m=0,l·n=0∴ l·g=0∴ l⊥g∴ l⊥g 这就证明了直线l垂直于平面内的任一条直线，所以l⊥ 巩固练习：利用向量知识证明三垂线定理aAOP .,0,,,,0,0,PAaPAaaOAaPOaPAOAyPOxPAyxOAPOOAPOaOAaOAaPOaPOPOaa即使有序实数对定理可知，存在唯一的不平行，由共面向量相交，得又又而上取非零向量证明：在PAaOAaaPAOAPAPO求证：且内的射影，在是的垂线，斜线，分别是平面已知：,,2019-12-294复习:2. 向量的夹角:abOABab0ab，ab，向量 的夹角记作:a b 与ab ||||cos,a bab 1.空间向量的数量积:111222( ,,), ( ,,)a xyzb xyz设12121 2xxyyzzcos||||ababa b ，1 21 21 2222222111222...