第5章单自由度系统振动

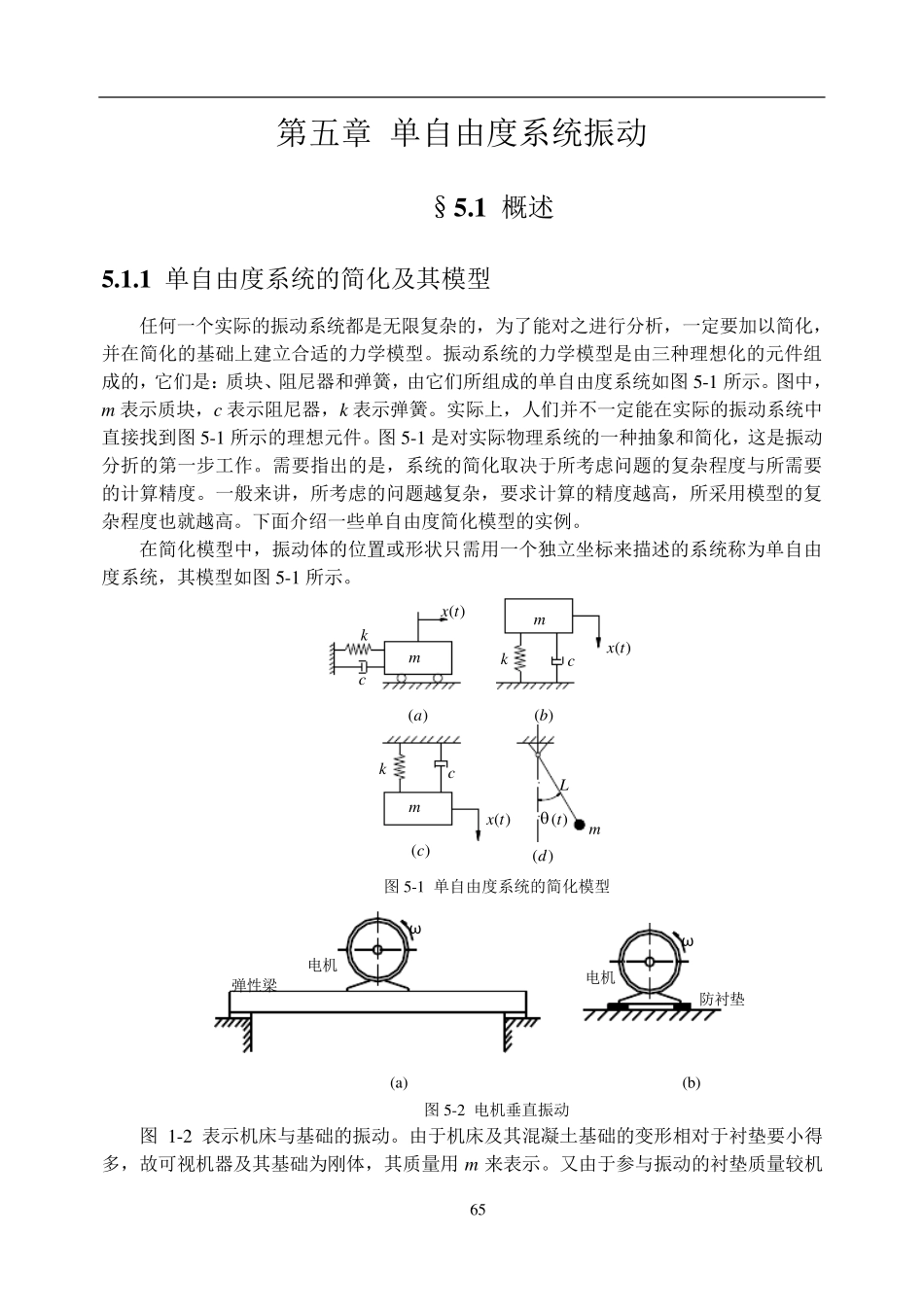
65 第五章 单自由度系统振动 §5 .1 概述 5 .1 .1 单自由度系统的简化及其模型 任何一个实际的振动系统都是无限复杂的，为了能对之进行分析，一定要加以简化，并在简化的基础上建立合适的力学模型。振动系统的力学模型是由三种理想化的元件组成的，它们是：质块、阻尼器和弹簧，由它们所组成的单自由度系统如图 5-1 所示。图中，m 表示质块，c 表示阻尼器，k 表示弹簧。实际上，人们并不一定能在实际的振动系统中直接找到图 5-1 所示的理想元件。图 5-1 是对实际物理系统的一种抽象和简化，这是振动分折的第一步工作。需要指出的是，系统的简化取决于所考虑问题的复杂程度与所需要的计算精度。一般来讲，所考虑的问题越复杂，要求计算的精度越高，所采用模型的复杂程度也就越高。下面介绍一些单自由度简化模型的实例。 在简化模型中，振动体的位置或形状只需用一个独立坐标来描述的系统称为单自由度系统，其模型如图 5-1 所示。 kckckc)(tx)(tx)(tx)(tLmmmm)(a)(b)(c)(d 图 5-1 单自由度系统的简化模型 防衬垫电机ωω电机弹性梁 (a) (b) 图 5-2 电机垂直振动 图 1-2 表示机床与基础的振动。由于机床及其混凝土基础的变形相对于衬垫要小得多，故可视机器及其基础为刚体，其质量用 m 来表示。又由于参与振动的衬垫质量较机 66 器及其基础要小得多，且衬垫较软，具有能耗作用，可视为弹簧和阻尼器，则图1-2 所示的系统即可简化为图5-1(b)所示的单自由度系统。显然这种简化的结果只能用于研究机器及其基础在垂直方向上的整机振动。又如图5-2(a)所示安装在弹性梁上与图5-2(b)所示安装在防振垫(橡皮、木块等)上的电机若只研究电机在垂直方向上的振动也可简化为图5-1(b)所示的单自由度系统。 图5-3 所示的连杆，当研究连杆的角振动θ (t)时，若将连杆的分布质量演化为其质心在c 处的集中质量 m，则可简化为图5-l(d)所示的单摆系统。图5-7所示飞轮的扭转振动，由于飞轮的惯性矩相对于轴的惯性矩要大好多，可将轴简化为一扭转弹簧，从而得到单自由度扭振系统，该系统以角度θ 为坐标，又称为角振动系统。 o)(tmLc kLIG, 图5-3 连杆角振动 图5-4 飞轮扭转振动 下面介绍组成振动系统的各种理想元件的意义与性质。 一、弹性元件 1 .弹性元件的意义与性质 在振动系统中，弹性元件(或弹簧)对于外力作用的响应，表现为一定的位移或变形。图5-5(a)为弹性元件的示意图。弹簧所受外力 Fs是位移 x...