第5章频率法

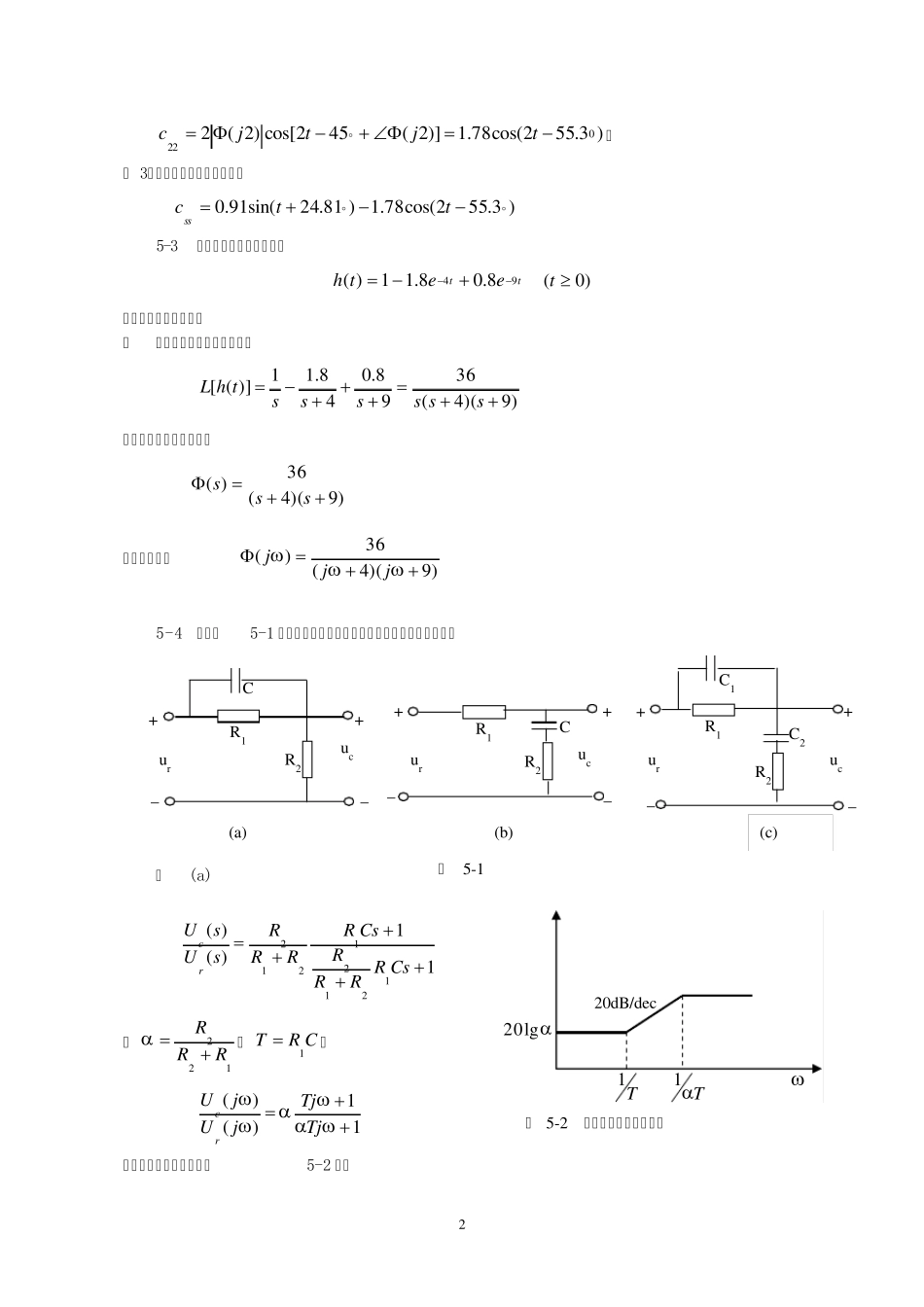
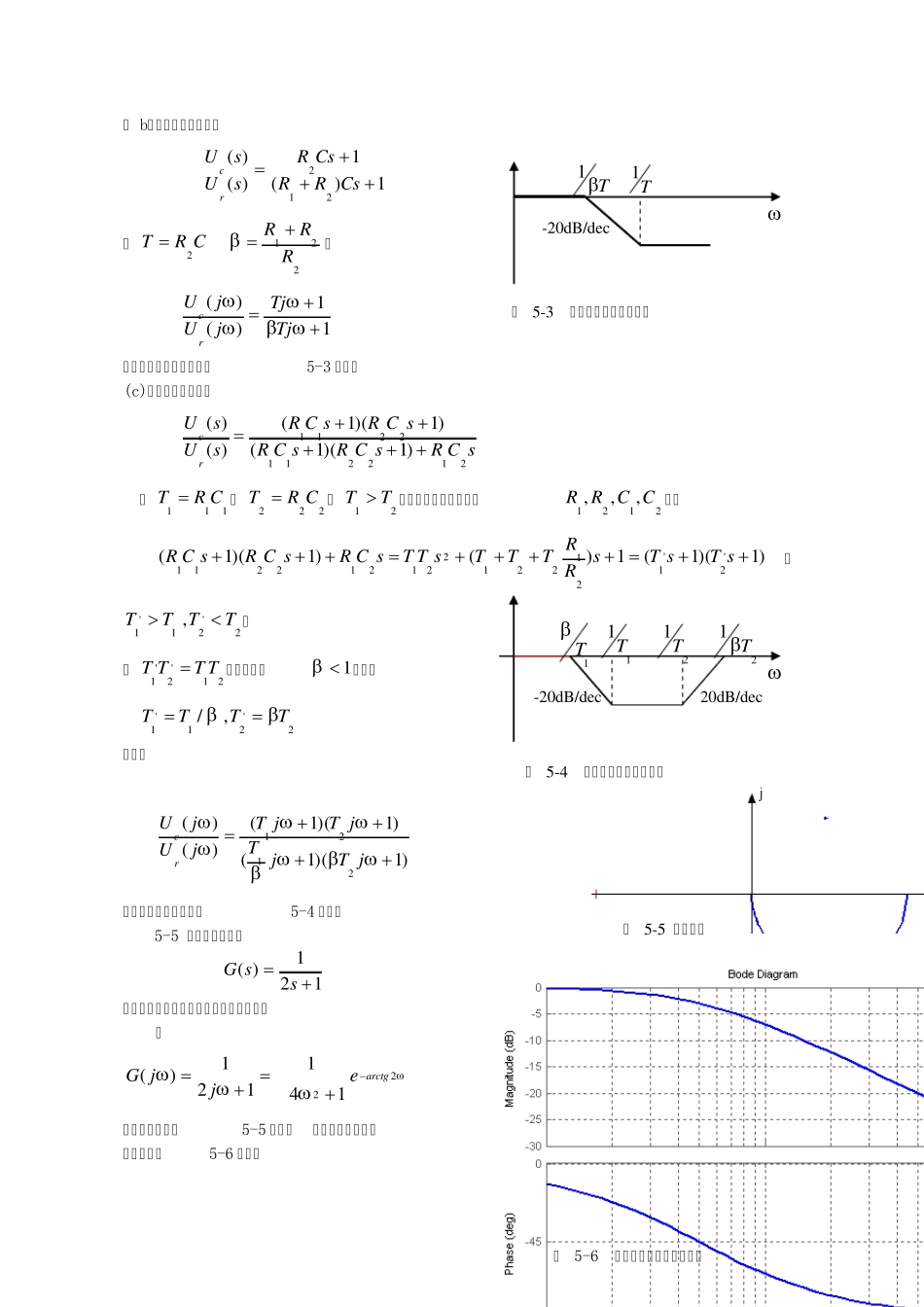
1 5-1 某放大器的传递函数如下 1)( TsKsG 今测得其频率响应，当srad /1时，幅频A=12/2，相频4。问放大系数K 及时间常数 T 各为多少。 解 当srad /1时 62121)1(2TKjG 4)1(arctgTjG 由上述两式得 sT1，26K。 5-2 设单位负反馈控制系统的开环传递函数110)( ssG， 当下列输入信号作用在闭环系统上时，求系统的稳态输出ssc 。 （ 1）)30sin()(ttr （ 2）)452cos(2)(ttr （ 3）)452cos(2)30sin()(tttr 解 （ 1）系统的闭环传递函数为 1110)(ss 由输入信号的表达式可知srad /1。当srad /1时，幅值及相角分别为 91.011110)1(2 j 19.5111)1(arctgj 系统的稳态输出为 )81.24sin(91.0)]1(30sin[)1(tjtjcss （ 2）由输入信号的表达式可知srad /2。当srad /2时，幅值及相角分别为 89.011210)2(22 j 3.10112)1(arctgj 稳态输出为 2 )3.552cos(78.1)]2(452cos[)2(2022tjtjc。 （ 3）根据线性系统叠加原理得 )3.552cos(78.1)81.24sin(91.0ttcss 5-3 若系统的单位阶跃响应为 tteeth948.08.11)( )0( t 试求系统的频率特性。 解 对阶跃响应进行拉氏变换得 )9)(4(3698.048.11)]([ssssssthL 则系统的闭环传递函数为 )9)(4(36)(sss 系统频率特性 )9)(4(36)(jjj 5-4 试求图5-1 所示网络的频率特性，并画出其对数幅频渐近线。 解 (a) 11)()(12121212CsRRRRCsRRRRsUsUrc 令122RRR，CRT1则 11)()(TjTjjUjUrc 其对数幅频渐近特性如图5-2 所示 R1 R2 C + + _ _ u c u r + R2 R1 + _ _ C1 C2 u c u r _ R1 R2 + + _ C u c u r (a) (b) (c) 图 5-1 lg20T1T120dB/dec 图 5-2 对数幅频渐近特性曲线 3 （ b）网络的传递函数为 1)(1)()(212CsRRCsRsUsUrc 令CRT2 221RRR 则 11)()(TjTjjUjUrc 其对数幅频渐近特性如图5-3 所示。 (c)网络的传递函数为 sCRsCRsCRsCRsCRsUsUrc2122112211)1)(1()1)(1()()( 令111CRT ，222CRT 且21TT ，为简化问题的分析设2121,,,CCRR满足 )1)(1(1)()1)(1('2'...