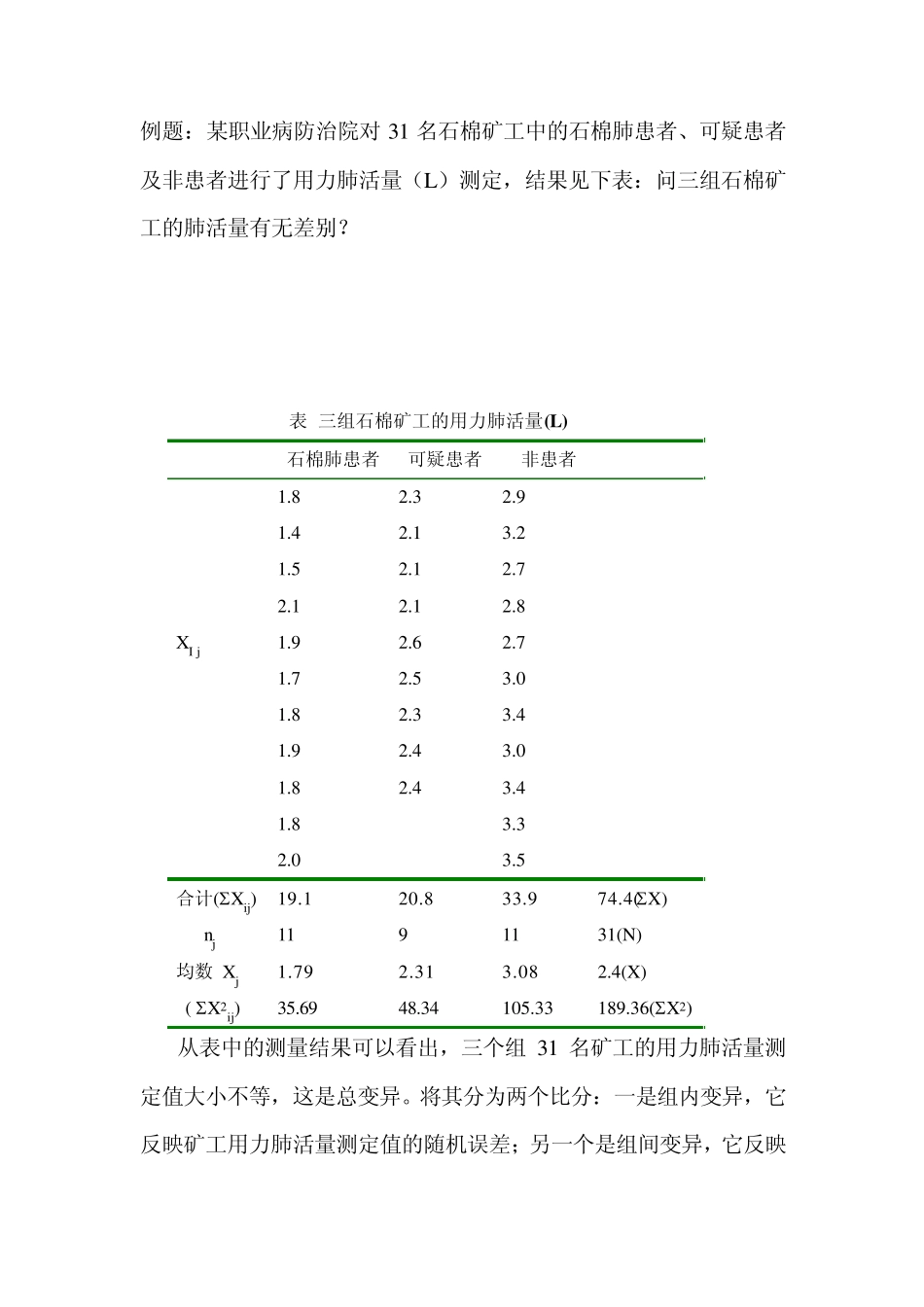
方差分析 方差分析(analysis of variance ), 简称ANOVA, 由英国统计学家R.A.Fisher 首先提出,后人为纪念Fisher ,以F 命名方差分析的统计量,故方差分析又称F 检验。 样本均数的差异,可能有两种原因所致。首先可能由随机误差所致随机误差包括两种成分:个体间的变异和测量误差两部分;其次可能是由于各组所接受的处理不同,不同的处理引起不同的作用和效果,导致各处理组之间均数不同。一般来说,个体之间各不相同,是繁杂的生物界的特点;测量误差也是不可避免的,因此第一种原因肯定存在。而第二种原因是否存在,这正是假设检验要回答的问题。 方差分析的基本思想是将所有观察值之间的变异(称总变异)按设计和需要分解成几部分。如完全随机设计资料的方差分析,将总变异分解为处理间变异和组内变异两部分,后者常称为误差。将各部分变异除以误差部分,得到统计量F 值,并根据 F 值确定 P 值作推断。 由于方差分析是根据实验设计将总变异分成若干部分,因此设计时考虑的因素越多,变异划分的越精细,各部分变异的涵义越清晰明确,结论的解释也越容易,同时由于变异划分的精细,误差部分减小,提高了检验的灵敏度和结论的准确性。 方差分析可用于: (1)两个或多个样本均数间的比较 (2)分析两个或多个因素的交互作用 (3)回归方程的假设检验 (4)方差齐性检验 多个样本均数间比较的方差分析应用条件为: (1)各样本必须是相互独立的随机样本(独立性) (2)各样本均来自正态总体(正态性) (3)相互比较的各样本的总体方差相等(方差齐性) 一、完全随机设计的方差分析 医学实验中,根据某一实验因素,用随机的方法,将受试对象分配到各组,各组分别接受不同的处理后,观察各种处理的效果,比较各组均数之间有无差别。临床研究中,还可能遇到:比较几种不同疗法治疗某种疾病后某指标的变化,以评价它们的疗效;或比较某种疾病不同类型之间某一指标有无差别等。这些都是一个因素不同水平(或状态)间几个样本均数的比较,可用单因素的方差分析(one-way ANOVA)来处理此类资料。 例题:某职业病防治院对31 名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量(L)测定,结果见下表:问三组石棉矿工的肺活量有无差别? 表 三组石棉矿工的用力肺活量(L ) 石棉肺患者 可疑患者 非患者 1.8 2.3 2.9 1.4 2.1 3.2 1.5 2.1 2.7 2.1 2.1 2.8 XI j 1.9 2.6 2.7 1.7 2.5 3.0...