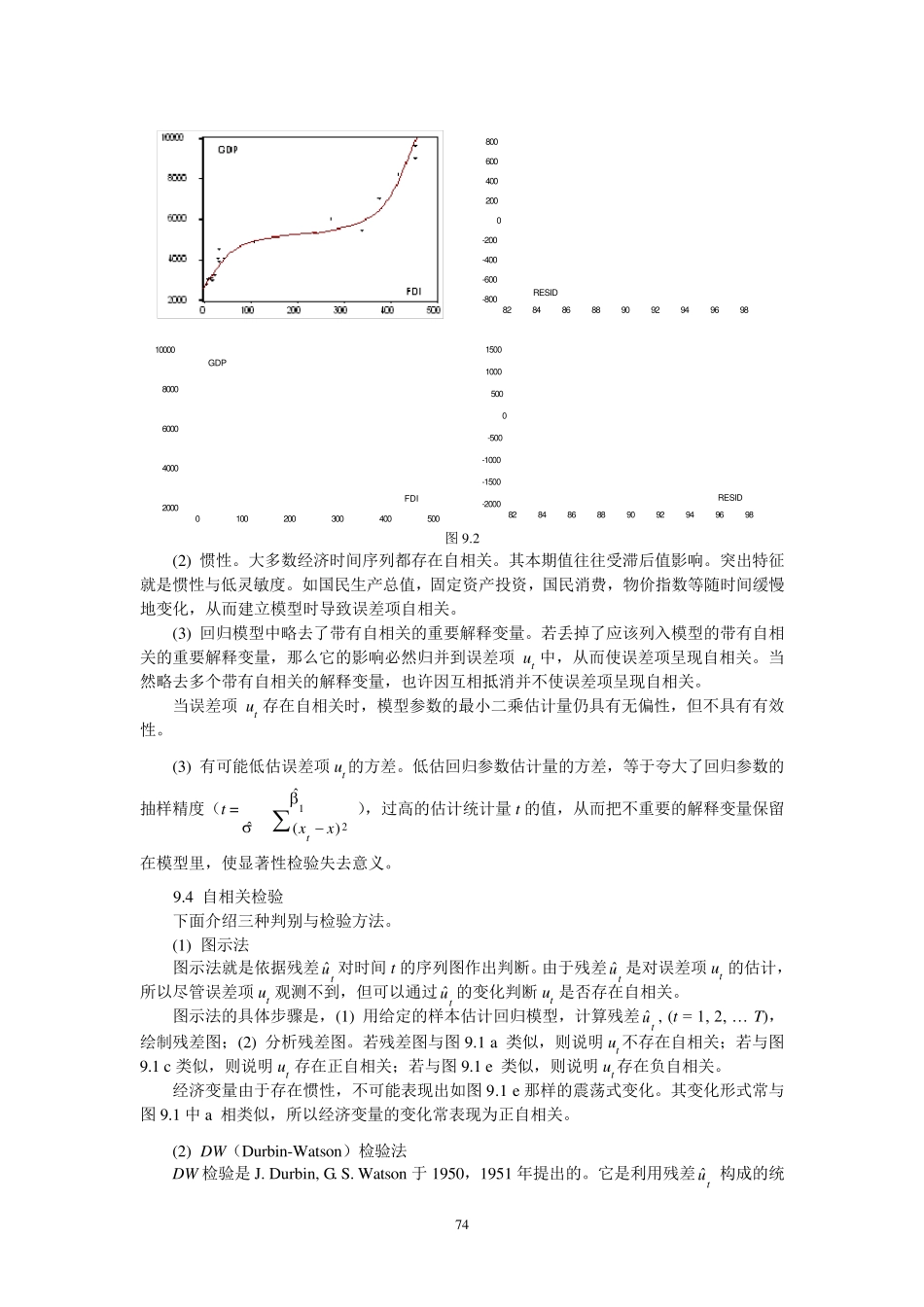
72 第9 讲 自相关检验 9.1 非自相关假定 由第2 章知回归模型的假定条件之一是, Co v (ui, uj ) = E(ui uj) = 0, (i, j T, i j), (9.1) 即误差项ut 的取值在时间上是相互无关的。称误差项ut 非自相关。如果 Co v (ui , uj ) 0, (i j) 则称误差项ut 存在自相关。 自相关又称序列相关。原指一随机变量在时间上与其滞后项之间的相关。这里主要是指回归模型中随机误差项ut 与其滞后项的相关关系。自相关也是相关关系的一种。 9.2 一阶自相关 通常假定误差项的自相关是线性的。因计量经济模型中自相关的最常见形式是一阶自回归形式,所以下面重点讨论误差项的线性一阶自回归形式,即 ut = 1 ut -1 + vt (9.2) 其中1 是自回归系数,vt 是随机误差项。vt 满足通常假设。 依据普通最小二乘法公式,模型(9.2)中 1 的估计公式是, 1ˆa = TttTtttuuu22121 (1ˆ =2)())((xxxxyyttt) (9.3) 其中T 是样本容量。若把ut, u t-1 看作两个变量,则它们的相关系数是 ˆ = TttTttTtttuuuu2212221 (r =TttTttTtttxxyyxxyy12121)()())(() (9.4) 对于大样本显然有 Tttu22 Tttu221 (9.5) 把上关系式代入(9.4)式得 ˆ ≈ TttTtttuuu22121 = 1ˆa (9.6) 因而对于总体参数有 = 1,即一阶自回归形式的自回归系数等于该二个变量的相关系数。因此原回归模型中误差项ut 的一阶自回归形式(见模型(9.2))可表示为, ut = ut-1 + vt. (9.7) 的取值范围是 [-1,1]。当 0 时,称ut 存在正自相关;当 0 时,称ut 存在负自相关。当 = 0 时,称ut 不存在自相关。图 9.1 a, c, e, 分别给出具有正自相关,负自相关和非自相关的三个序列。为便于理解时间序列的正负自相关特征,图 9.1 b, d, f, 分别给出图 9.1 a, c, e, 中变量对其一阶滞后变量的散点图。正负自相关以及非自相关性展现的更为明了。 73 -3-2-10123102030405060708090100U -4-2024-4-2024U(-1)U a. 非自相关的序列图 b. 非自相关的散点图 -4-2024102030405060708090100X -6-4-20246-6-4-20246X(-1)X c. 正自相关的序列图 d. 正自相关的散点图 -6-4-20246102030405060708090100X -6-4-20246-6-4-20246X(-1)X e. 负自...