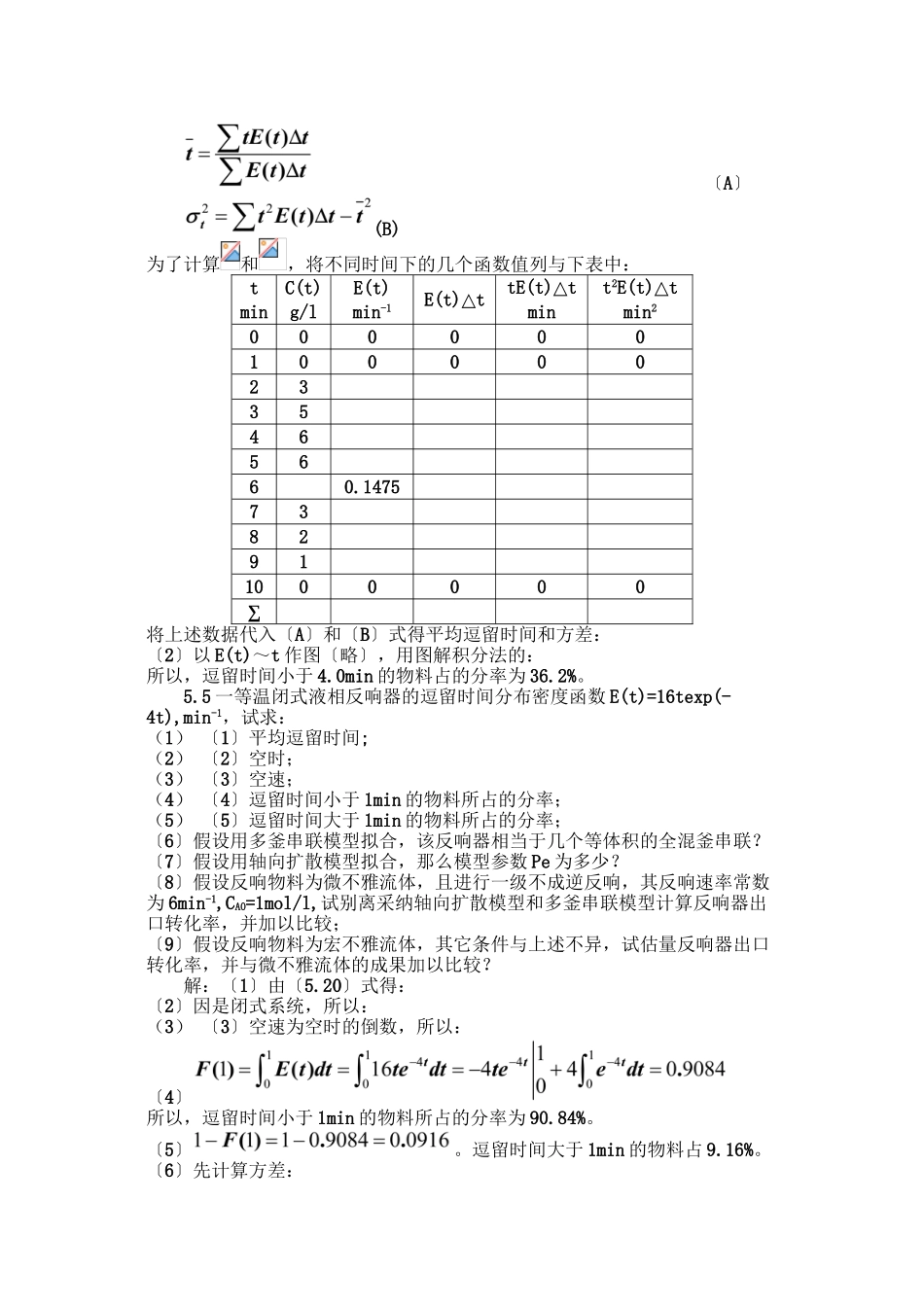
5 逗留时间分布与反响器5.1 设 F(θ)及 E(θ)别离为闭式流动反响器的逗留时间分布函数及逗留时间分布密度函数,θ 为比照时间。(1) 〔1〕假设该反响器为活塞流反响器,试求(a) 〔a〕F(1)(b)E(1)(c)F(0.8)(d)E(0.8)(e)E(1.2)(2)假设该反响器为全混流反响器,试求〔a〕F(1)(b)E(1)(c)F(0.8)(d)E(0.8)(e)E(1.2)(3) 假设该反响器为一个非理想流动反响器,试求〔a〕F(∞)(b)F(0)(c)E(∞)(d)E(0)(e)(f)解:〔1〕因是活塞流反响器,故符合理想活塞流模型的逗留时间分布,由〔5.33-5.36〕式可得:(a)F(1)=1.0(b)E(1)=∝(c)F(0.8)=0(d)E(0.8)=0(e)E(1.2)=0(2) 〔2〕因是全混流反响器,故符合理想全混流模型的逗留时间分布,由〔5.33-5.36〕式可得:〔a〕F(1)=1-e-1=0.6321 (b)E(1)=e-1=0.3679 (c)F(0.8)=1- e=0.5507 (d)E(0.8)= e012(3) 〔3〕因是一个非理想流动反响器,故可得:〔a〕F(∞)=1 (b)F(0)=0 (c)E(∞)=0 (d)E(0)>1 (e)=1 (f) =15.2 用阶跃法测定一闭式流动反响器的逗留时间分布,得到离开反响器的示踪剂与时间的关系如下:试求:(1) 〔1〕该反响器的逗留时间分布函数 F(θ)及分布密度函数 E(θ)。(2) 〔2〕数学期望及方差。(3) 〔3〕假设用多釜串联模型来模拟该反响器,那么模型参数是多少?(4) 〔4〕假设用轴相扩散模型来模拟该反响器,那么模型参数是多少?〔5〕假设在此反响器内进行一级不成逆反响,反响速率常数 k=1min-1,且无副反响,试求反响器出口转化率。解:〔1〕由图可知 C0=C(∝)=1.0,而 F(θ)=F(t)=C(t)/ C(∝),所以:如以下图所示:由〔5.20〕式可得平均逗留时间:即为上图中暗影面积。由〔5.5〕式得:所以:如右图所示:〔2〕由于是闭式系统,故,所以由式〔5.23〕可得方差:〔3〕由〔5.20〕式可得模型参数 N 为:(4) 〔4〕由于返混很小,故可用,所以:〔5〕用多釜串联模型来模拟,前已求得 N=75,应用式〔3.50〕即可计算转化率:同理,亦可用扩散模型即〔5.69〕式得 XA=0.9146。两种方法计算成果相当吻合。5.3 用阶跃法测定一闭式流动反响器的逗留时间分布,得到离开反响器的示踪剂与时间的关系如下:t,s01525354555657590100C(t),g/cm30(1) 〔1〕试求该反响器的逗留时间分布及平均逗留时间。-1,估计反响器出口处的转化率。〔3〕假设反响器内的物料为宏不雅流体,其它条件均不变,试问反响器出口处的转化率又是多少?解:〔1〕由式〔5.17〕计算出反响器的逗留时...