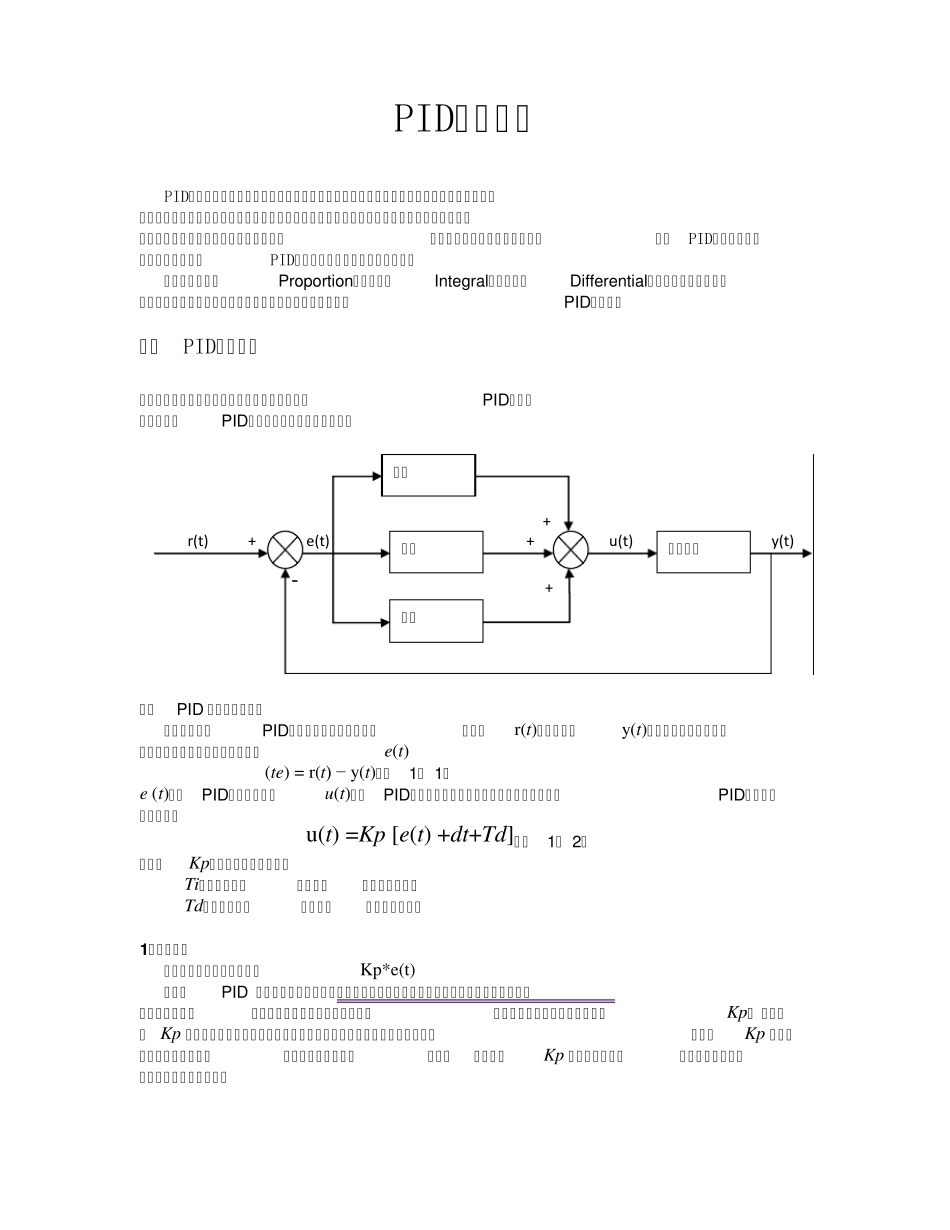
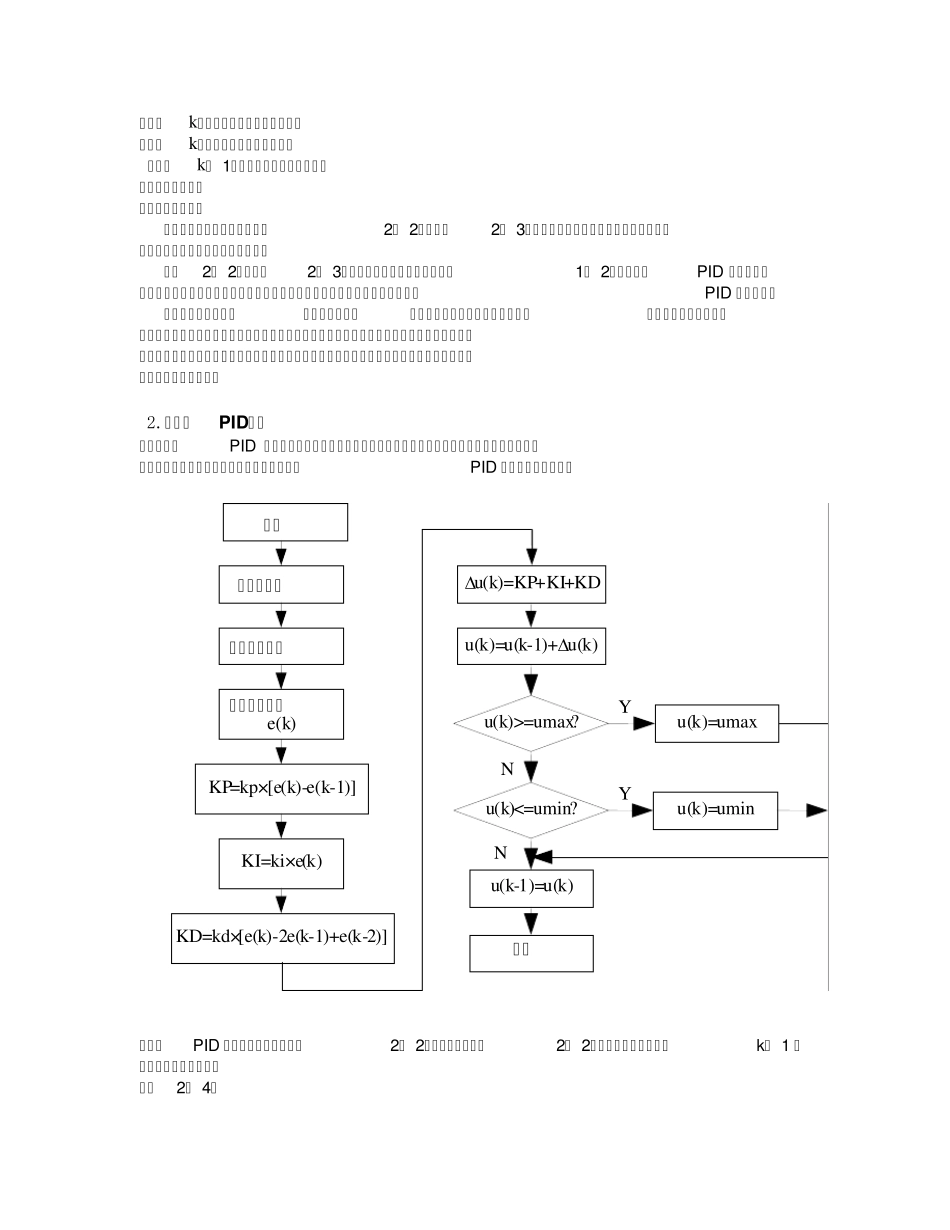
PID控制原理 PID算法是最早发展起来的控制策略之一,由于其算法简单、鲁棒性(系统抵御各种扰动因素——包括系统内部结构、参数的不确定性,系统外部的各种干扰等的能力)好及可靠性高而被广泛地应用于过程控制和运动控制中。尤其是随着计算机技术的发展,数字PID控制被广泛地加以应用,不同的PID控制算法其控制效果也各有不同。 将偏差的比例(Proportion)、积分(Integral)和微分(Differential)通过线性组合构成控制量,用这一控制量对被控对象进行控制,这样的控制器称PID控制器。 模拟PID控制原理 在模拟控制系统中,控制器最常用的控制规律是PID控制。 常规的模拟PID控制系统原理框图如图所示。 + r(t) + e(t) + u(t) y(t) - + 模拟PID 控制系统原理图 该系统由模拟PID控制器和被控对象组成。图中, r(t)是给定值, y (t)是系统的实际输出值,给定值与实际输出值构成控制偏差e(t) (te) = r(t) − y (t)(式1- 1) e (t)作为PID控制的输入,u (t)作为PID控制器的输出和被控对象的输入。所以模拟PID控制器的控制规律为 u (t) =Kp [e(t) +dt+Td](式1- 2) 其中:Kp――控制器的比例系数 Ti--控制器的积分时间,也称积分系数 Td――控制器的微分时间,也称微分系数 1、比例部分 比例部分的数学式表示是:Kp*e(t) 在模拟PID 控制器中,比例环节的作用是对偏差瞬间作出反应。偏差一旦产生控制器立即产生控制作用,使控制量向减少偏差的方向变化。控制作用的强弱取决于比例系数Kp, 比例系数 Kp 越大,控制作用越强,则过渡过程越快,控制过程的静态偏差也就越小;但是Kp 越大,也越容易产生振荡,破坏系统的稳定性。故而,比例系数Kp 选择必须恰当,才能过渡时间少,静差小而又稳定的效果。 比例 积分 微分 被控对象 2、积分部分 积分部分的数学式表示是: 从积分部分的数学表达式可以知道,只要存在偏差,则它的控制作用就不断的增加;只有在偏差 e(t)=0 时,它的积分才能是一个常数,控制作用才是一个不会增加的常数。可见,积分部分可以消除系统的偏差。 积分环节的调节作用虽然会消除静态误差,但也会降低系统的响应速度,增加系统的超调量。积分常数Ti 越大,积分的积累作用越弱,这时系统在过渡时不会产生振荡;但是增大积分常数会减慢静态误差的消除过程,消除偏差所需的时间也较长,但可以减少超调量,提高系统的稳定性。当Ti 较小时,则积分的作用较强,这时系统过...