自考概率论与数理统计基础知识

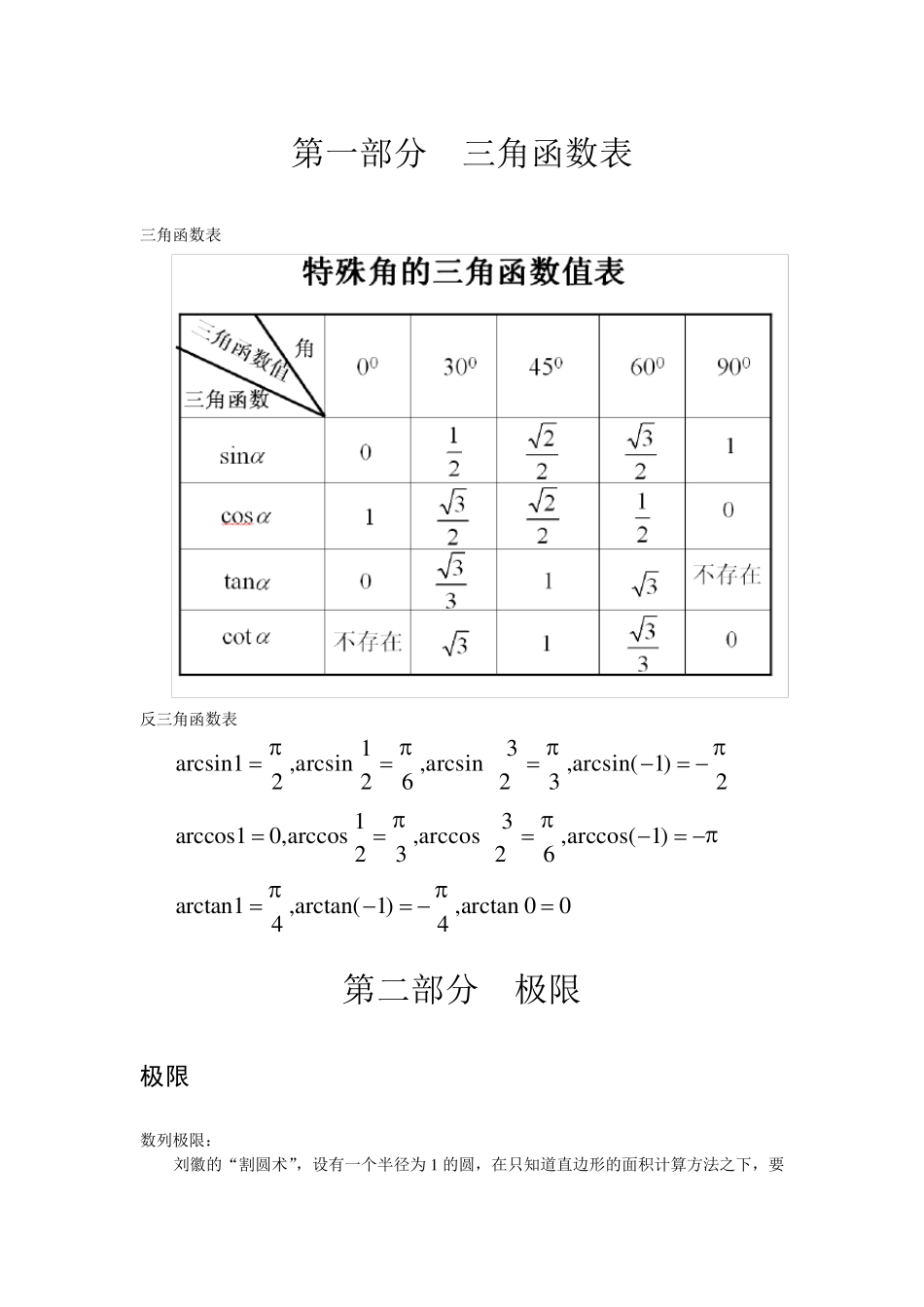
第一部分 三角函数表 三角函数表 反三角函数表 13arcsin1,arcsin,arcsin,arcsin( 1)226232  13arccos10,arccos,arccos,arccos( 1)2326  arctan1,arctan( 1),arctan 0044  第二部分 极限 极限 数列极限： 刘徽的“割圆术”，设有一个半径为 1 的圆，在只知道直边形的面积计算方法之下，要计算其面积： 方法：先做圆的内接正六边形，其面积记为1A ，再做一内接正12 边形，记其面积为2A再做一内接正24 边形，记其面积为3A ,如此逐次将变数加倍。。。 得到数列12,,...,,.....nA AA，则当 n 无穷大时，有limnnAs 函数极限： 00lim( )()xxf xf x 常用的极限公式 0lim0(0)lim0(0)1xxxxeeeee 1lim0lim arctan2lim arctan2nxxnxx  常用的几个公式 (1)12...2n nn 111111()1(1)11nnkkk kkkn  21......2!!nxxxexn  等比数列公式：是等比数列 ,nS 1(1)1naqq 当 q<1 时，等比数列的无穷项级数和为 11aSq  等差数列公式：1()2nn aaSn 或者：1(1)2n ndSnna 例 设二维随机变量),(YX的分布函数为 )2arctan)(arctan(),(ycxbayxF,.,yx 求：（1）常数a, b, c; (2) ),(YX的概率密度. 解：（1）由分布函数的性质知 ,0))2arctan()(2(),(,0)2))(arctan((),(,1)2)(2(),(ycbayFcxbaxFcbaF 从上面第二式得2c, 从上面第三式 得2b, 再从上面第一式 得21a. 由于,)2arctan2)(arctan2(1),(2yxyxF 从而概率密度为 .)41)(1(2),(),(2222yxyxyxFyxf 第三部分 导数 导数含义 函数值的增长与自变量增长之比的极限。 重要的求导公式 ( )0.C  1()nnxnx  ()lnxxaaa. ()xxee 1(log)lna xxa． 1(ln )xx． (sin )cosxx． (cos )sinxx ． 222211(arcsin)(arccos)1111(arctan)(arc cot)1111(log)(ln)lnaxxxxxxxxxxxax   导数的四则运算 若函数 )(xuu ， )(xvv 都在点x 处可导，则有 (ⅰ))()())()((xvxuxvxu； (ⅱ))()()()(])()([xvxuxvxuxvxu； ...