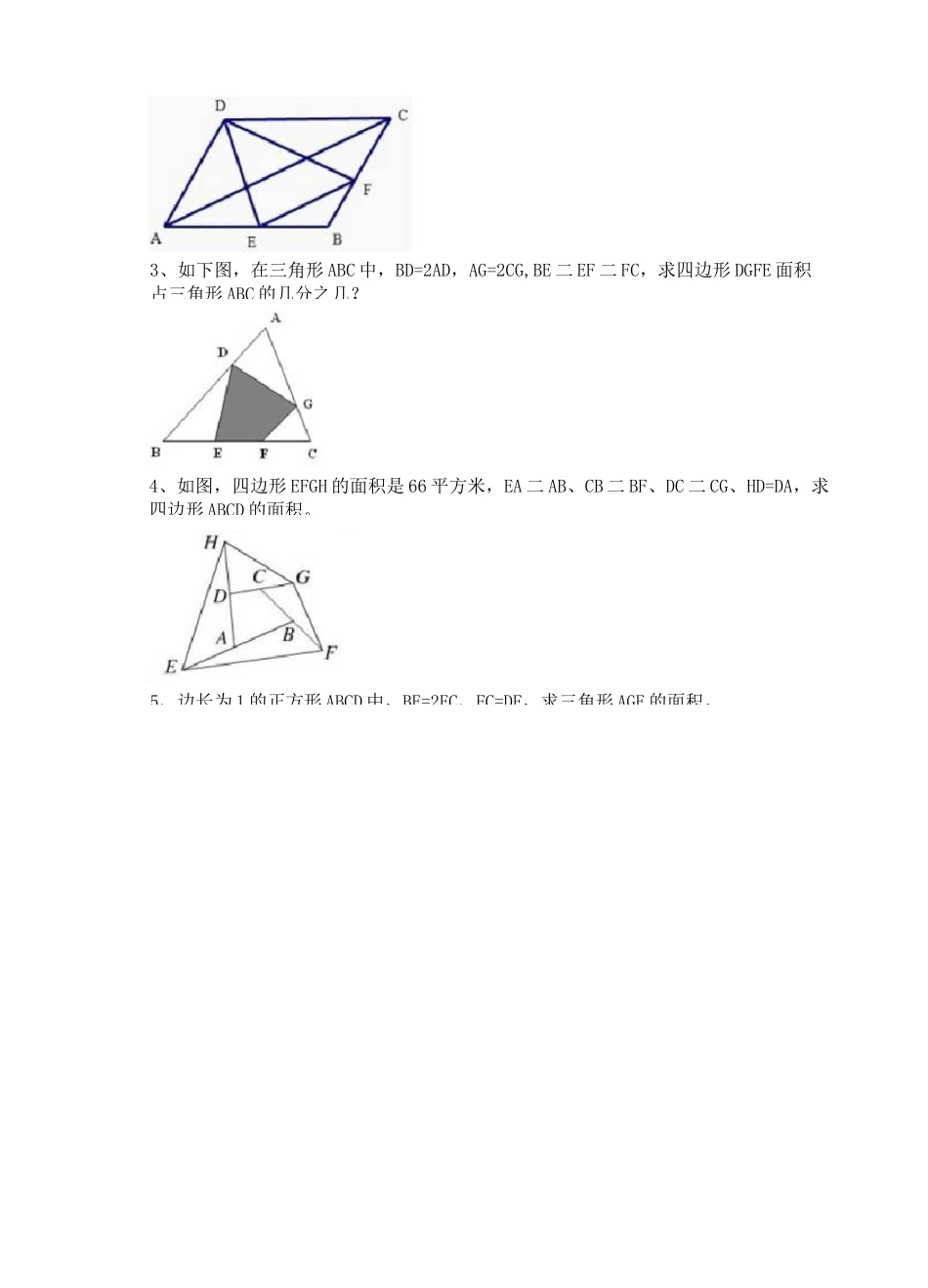
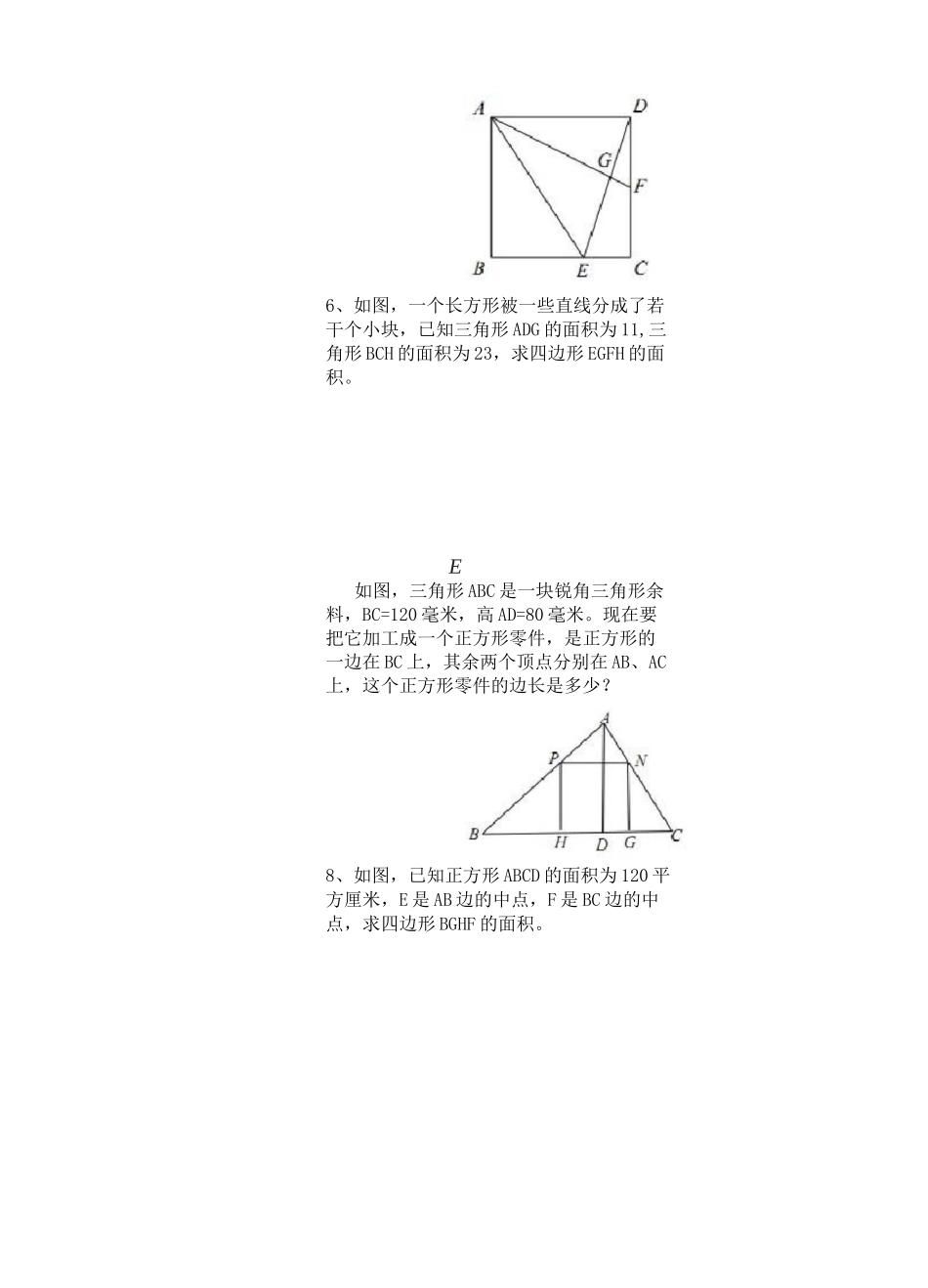
奥数】小升初几何五大模型巩固练习1、如图,在角 MON 的两边上分别有 A、C、E、B、D、F 六个点,并且AOAB、△ABC.△BCD、ACDE、ADEF 的面积都等于 1,求厶 DCF 的面积。2、如下图,ABCD 为平行四边形,EF 平行AC,如果△ADE 的面积为 4 平方厘米,求三角形 CDF 的面积。巩固练习题3、如下图,在三角形 ABC 中,BD=2AD,AG=2CG,BE 二 EF 二 FC,求四边形 DGFE 面积占三角形 ABC 的几分之几?4、如图,四边形 EFGH 的面积是 66 平方米,EA 二 AB、CB 二 BF、DC 二 CG、HD=DA,求四边形 ABCD 的面积。5、边长为 1 的正方形 ABCD 中,BE=2EC、FC=DF,求三角形 AGE 的面积。6、如图,一个长方形被一些直线分成了若干个小块,已知三角形 ADG 的面积为 11,三角形 BCH 的面积为 23,求四边形 EGFH 的面积。E如图,三角形 ABC 是一块锐角三角形余料,BC=120 毫米,高 AD=80 毫米。现在要把它加工成一个正方形零件,是正方形的一边在 BC 上,其余两个顶点分别在 AB、AC上,这个正方形零件的边长是多少?8、如图,已知正方形 ABCD 的面积为 120 平方厘米,E 是 AB 边的中点,F 是 BC 边的中点,求四边形 BGHF 的面积。9、如图,正方形 ABCD 的边长是 12 厘米,E、F 分别是 AB、BC 的中点,AF 与 CE 交于点 G,求四边形 AGCD 的面积。DC【详解】如图所示,逹接驭 CE.因为平行四边形对谊平行,所以根据同底等高知,$远三=筠理>=§皿*同理*根据 AC.EF 平行,崩以「空=筠空 o所以,£叭—$5 尸 -4平方厘米 0【详解>i 个題 ife 们可以用等和变换来解’由于三角形 OCD 的面积是可以求岀的,所以只要求岀 0D;皿就能求出 ADGK 的面和。因为 3 皿=%叭*空=心’斯以曲冷%口=*3 弓;2.如下图,A0CD 为平行四边形.册平齐鸥如果 AADE 的面积为 4 平方厘米,求三角形口 T 的面积。K 如圍,ftfeiOW 的两边上分别有也口 E.B.D、F 六个点,井且△OAB、AABC.ABCD.ACDEx&KF 的面积都等于 1・求厶佃的面积。FCE0,巩固练习题解:122SREF【详解】根据鸟头模型的性质有;S^G=—K—ASAC3>如下图,在三角形 ABC 中,B22AD,AG=20G,BE=EF=FC,求四边形 DGFE 面和占三角形 ABC 的几分之几?4、如图"四 jJJKEFGH 的面和是閃平方米,论 HR、CB 注叭 DC=CG.HD=DA,求四边形 ABCD 的面歆.AEE亠BSLAGQ~^AGDF~~^AADF 二亍冥—=6:112由蝴蝶定理可得:"三2^SLAGE=...