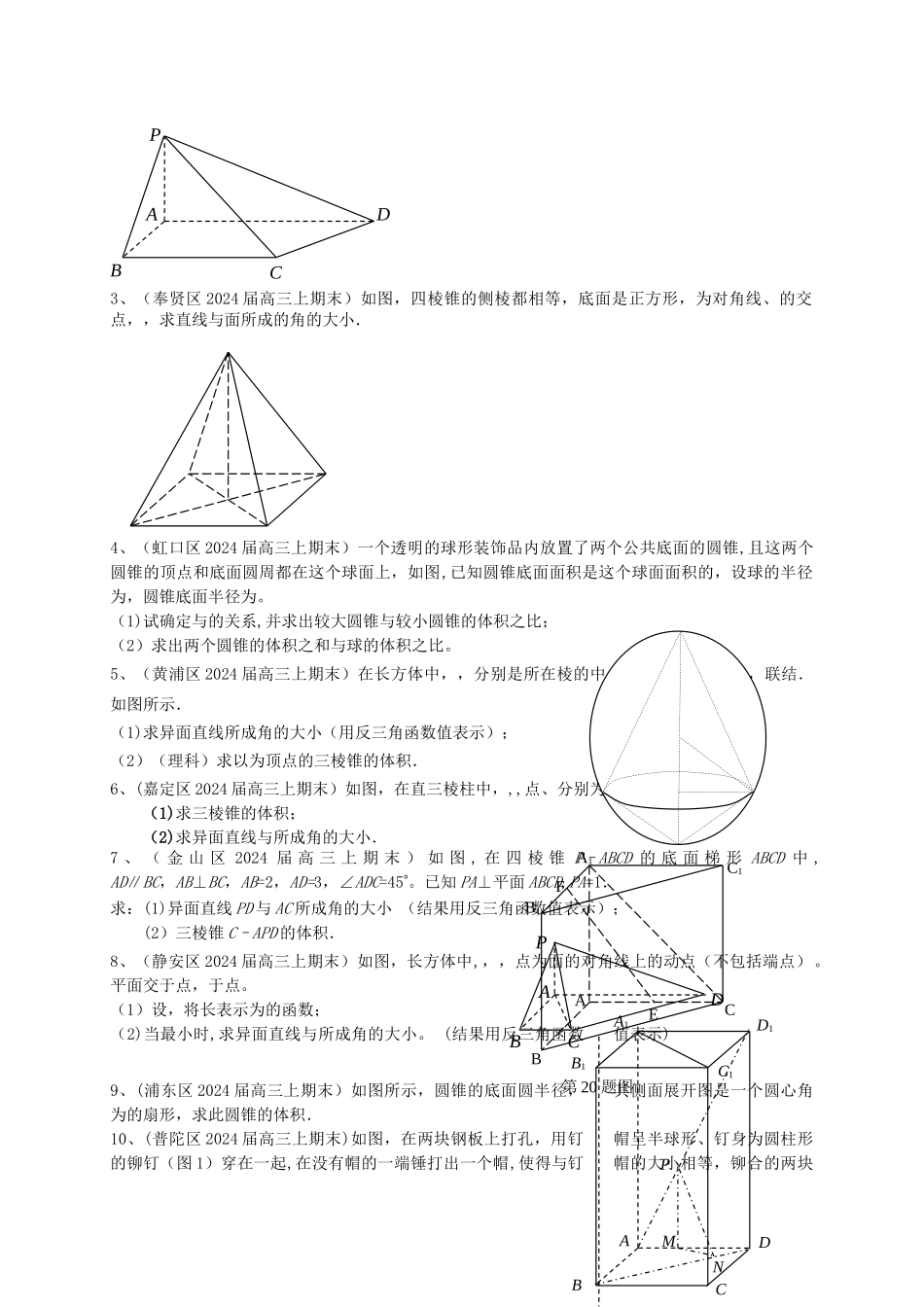
上海市各区县 2024 届高三上学期期末考试数学理试题分类汇编立体几何一、填空题1、(宝山区 2024 届高三上期末)正四棱锥的所有棱长均相等,是的中点,那么异面直线与所成的角的余弦值等于 2、(崇明县 2024 届高三上期末)圆锥的底面半径为 3,高为 1,则圆锥的侧面积为 3、(奉贤区 2024 届高三上期末)如图,在矩形中,为边的中点,,,分别以、为圆心,为半径作圆弧、(在线段上)。由两圆弧、及边所围成的平面图形绕直线旋转一周,则所形成的几何体的体积为 4、(虹口区 2024 届高三上期末)右图是正四面体的平面展开图,分别为的中点,则在这个正四面体中,与所成角的大小为 。5、(黄浦区 2024 届高三上期末)已知某圆锥体的底面半径,沿圆锥体的母线把侧面展开后得到一个圆心角为的扇形,则该圆锥体的表面积是 6、(嘉定区 2024 届高三上期末)若圆锥的侧面积是底面积的倍,则其母线与轴所成角的大小是____________(结果用反三角函数值表示).7、(金山区 2024 届高三上期末)如图所示,在长方体 ABCD–EFGH 中,AD=2,AB=AE=1,M 为矩形AEHD 内的一点,假如∠MGF=∠MGH,MG 和平面 EFG 所成角的正切值为,那么点 M 到平面 EFGH 的距离是 ▲ 8、(静安区 2024 届高三上期末)如图,在四棱锥中,已知底面,,底面是正方形,与底面所成角的大小为,则该四棱锥的体积是 。9、(浦东区 2024 届高三上期末)如图,已知平面,,,,、分别是、的中点。 则异面直线与所成角的大小为 。 10、(普陀区 2024 届高三上期末)如图,正三棱柱的底面边长为,体积为,则直线与底面 所成的角的大小为 (结果用反三角函数值表示).11、(松江区 2024 届高三上期末)在正四棱柱中,与平面所成的角为,则与所成的角为 ▲ ABCDPPCDE(结果用反三角函数表示).12、(徐汇区 2024 届高三上期末)若正四棱柱的底面边长为,高为,则异面直线与所成角的大小是______________.(结果用反三角函数值表示)13、(长宁区 2024 届高三上期末)如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是 二、选择题1、(奉贤区 2024 届高三上期末)在空间中,设、是不同的直线,、是不同的平面,且,,则下列命题正确的是 ( )A.若,则 B.若、异面,则、平行C.若、相交,则、相交 D.若,则 2、(青浦区 2024 届高三上期末)设是两条不同的直线,是两个不同的平面,则下面四个命题中错误的是……………...