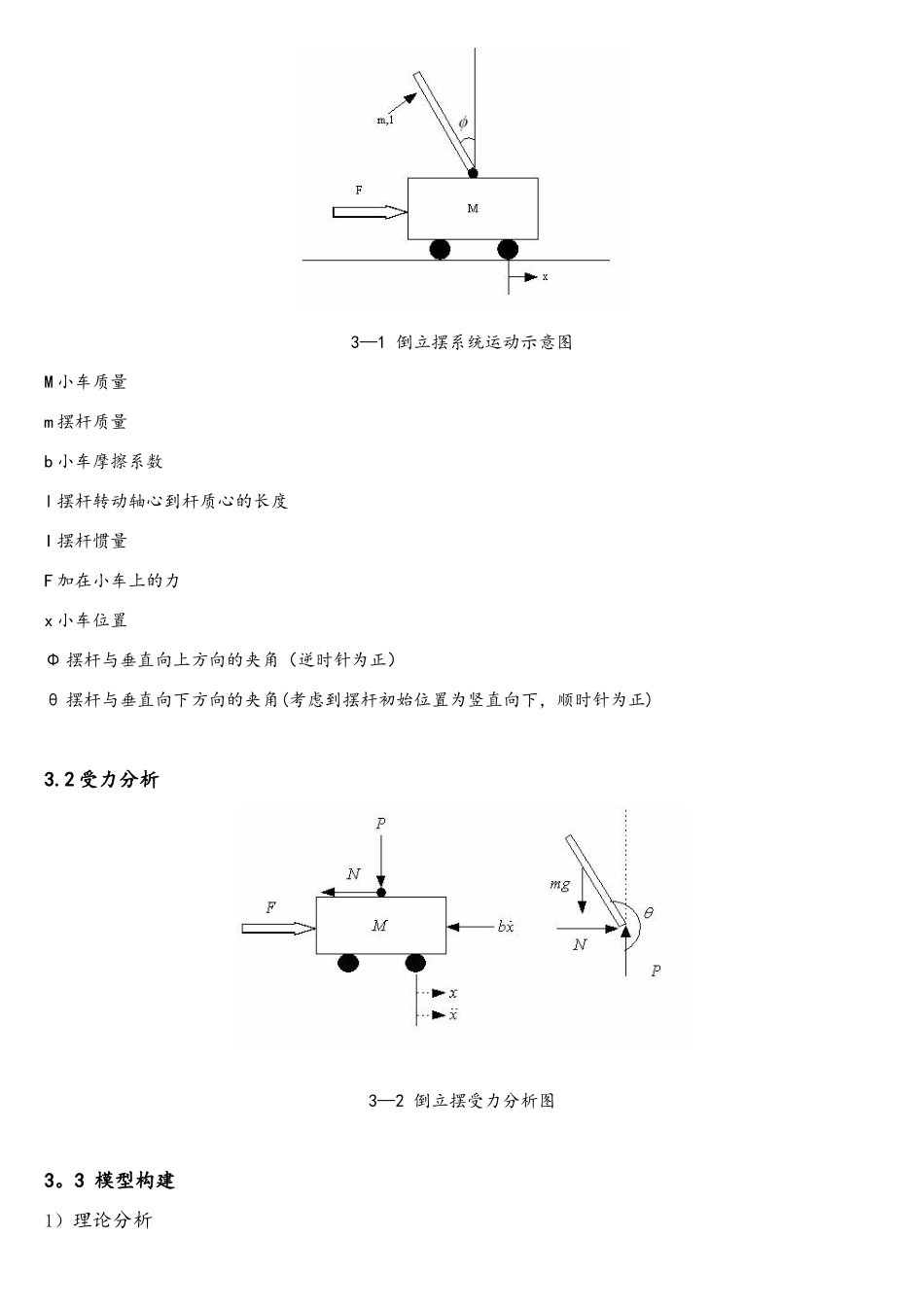
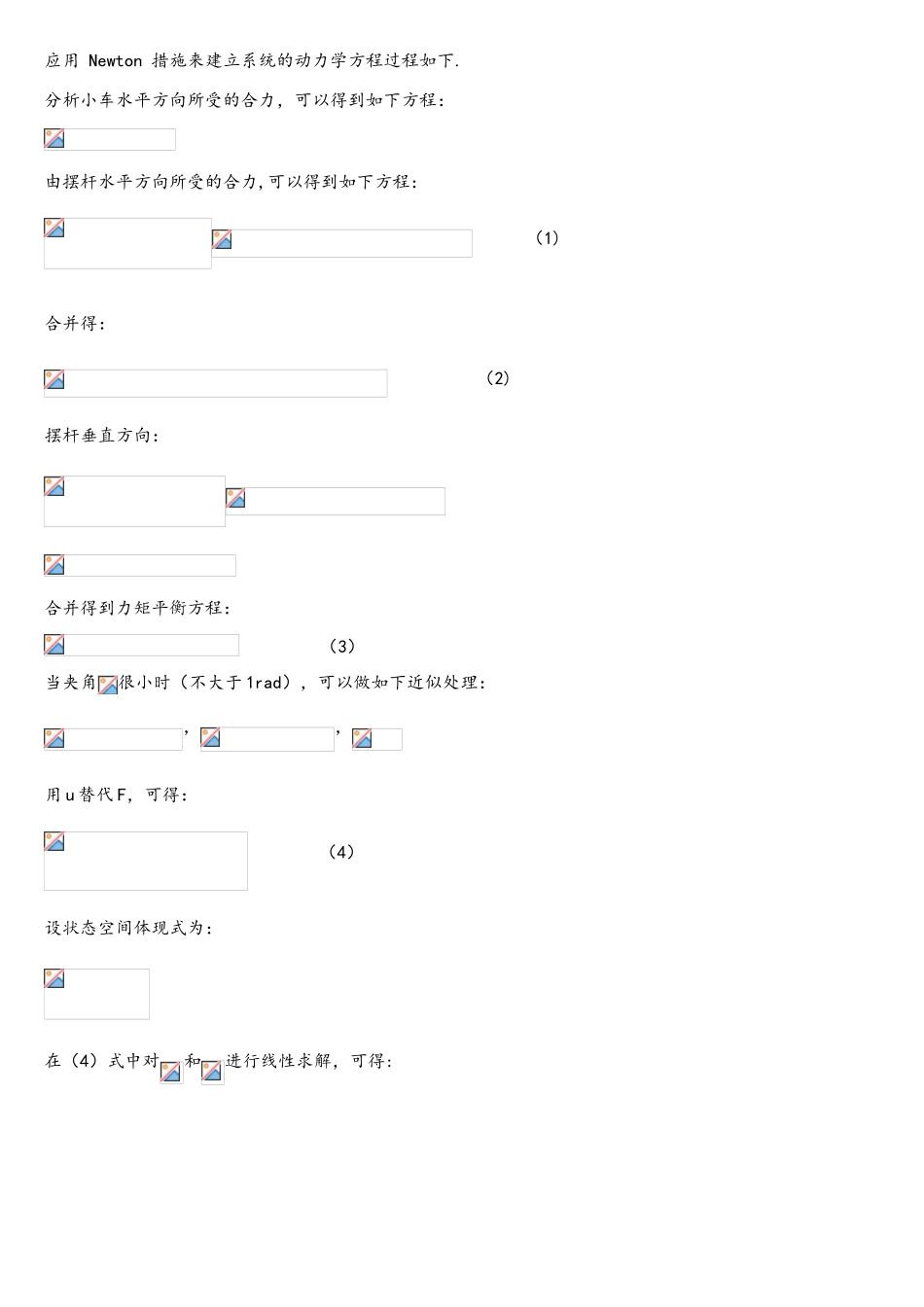
一级倒立摆研究(160232 蒋琴)1.背景简介倒立摆装置被公认为自动理论中的经典试验设备,也是控制理论教学和科研中不可多得的经典物理模型。通过倒立摆的研究,可以将控制理论所波及的三个基础学科:力学、数学和电学有机结合起来,在倒立摆中进行综合应用。在稳定控制问题上,倒立摆既具有普遍性又具有经典性。其构造简单,价格低廉,便于模拟和数字实现多种不一样的控制措施,倒立摆的控制措施有诸多种,如 PID、自适应、状态反馈、智能控制、模糊控制及神经元网络等多种理论和措施.用现代控制理论中的状态反馈措施来实现倒立摆系统的控制,就是设法调整闭环系统的极点分布,以构成闭环稳定的倒立摆系统,实际上,用线性化模型进行极点配置求得的状态反馈阵,不一定能使倒立摆稳定竖起来,能使倒立摆竖立起来的状态反馈阵是实际调试出来的,这个调试出来的状态反馈阵肯定满足极点配置。2.倒立摆简介倒立摆可以分为直线倒立摆、平面倒立摆和环形倒立摆等. 2—1 直线倒立摆 2—2 平面倒立摆 2—3 环形倒立摆3.模型构建3。1 倒立摆系统运动示意图3—1 倒立摆系统运动示意图M 小车质量m 摆杆质量b 小车摩擦系数l 摆杆转动轴心到杆质心的长度I 摆杆惯量F 加在小车上的力x 小车位置Φ 摆杆与垂直向上方向的夹角(逆时针为正)θ 摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下,顺时针为正)3.2 受力分析3—2 倒立摆受力分析图3。3 模型构建1)理论分析应用 Newton 措施来建立系统的动力学方程过程如下.分析小车水平方向所受的合力,可以得到如下方程: 由摆杆水平方向所受的合力,可以得到如下方程: (1) 合并得: (2) 摆杆垂直方向: 合并得到力矩平衡方程: (3)当夹角很小时(不大于 1rad),可以做如下近似处理:,, 用 u 替代 F,可得: (4)设状态空间体现式为:在(4)式中对和进行线性求解,可得: (5)其中:整理后,得到状态空间体现式为:+ (6)其中:2)实际问题实际系统参数如下:M 小车质量 1。096kgm 摆杆质量 0。109kgb 小车摩擦系数 0。1N/m/s 摆杆转动轴心到杆质心的长度 0.25m 摆杆惯量 0。0034T 采样时间 0.005s因此,状态空间体现式为: 3。4 系统的能观性和能控性能观性矩阵: 能控性矩阵: 因此,系统是能控能观的,自身即为最小系统.3。5 Simulink 仿真3—3 Simulink 仿真 3-4 小车位移输出图 3-5 摆杆角度输出图4.倒立摆试验4。1 倒立摆硬件系统构...