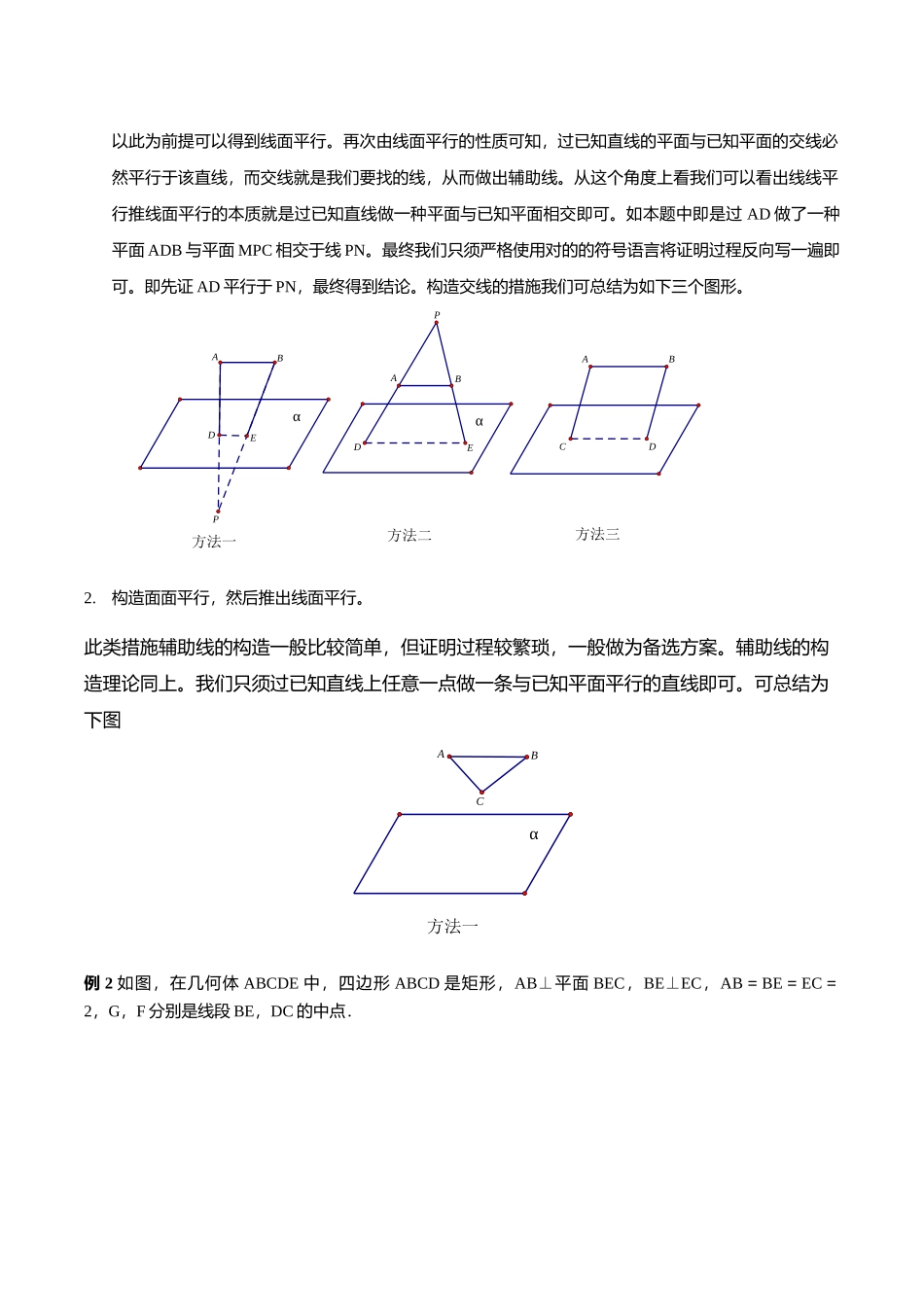
高考理科数学《立体几何》题型归纳与训练高考理科数学《立体几何》题型归纳与训练【题型归纳】题型一线面平行的证明例 1 如图,高为 1 的等腰梯形 ABCD 中,AM=CD=AB=1.现将△AMD 沿 MD 折起,使平面 AMD⊥平面 MBCD,连接 AB,AC.试判断:在 AB 边上与否存在点 P,使 AD∥平面 MPC?并阐明理由【答案】当 AP=AB 时,有 AD∥平面 MPC.理由如下:连接 BD 交 MC 于点 N,连接 NP.在梯形 MBCD 中,DC∥MB,==,在△ADB 中,=,∴AD∥PN. AD⊄平面 MPC,PN⊂平面 MPC,∴AD∥平面 MPC.【解析】线面平行,可以线线平行或者面面平行推出。此类题的难点就是怎样构造辅助线。构造完辅助线,证明过程只须注意规范的符号语言描述即可。本题用到的是线线平行推出面面平行。【易错点】不能对的地分析 DN 与 BN 的比例关系,导致成果错误。【思维点拨】此类题有两大类措施:1.构造线线平行,然后推出线面平行。此类措施的辅助线的构造须要学生理解线面平行的判定定理与线面平行的性质之间的矛盾转化关系。在此,我们需要借助倒推法进行分析。首先,此类型题目大部分为证明题,结论必然是对的的,我们以此为前提可以得到线面平行。再次由线面平行的性质可知,过已知直线的平面与已知平面的交线必然平行于该直线,而交线就是我们要找的线,从而做出辅助线。从这个角度上看我们可以看出线线平行推线面平行的本质就是过已知直线做一种平面与已知平面相交即可。如本题中即是过 AD 做了一种平面 ADB 与平面 MPC 相交于线 PN。最终我们只须严格使用对的的符号语言将证明过程反向写一遍即可。即先证 AD 平行于 PN,最终得到结论。构造交线的措施我们可总结为如下三个图形。方法三方法二方法一ααPABPABDEABCDDE2.构造面面平行,然后推出线面平行。此类措施辅助线的构造一般比较简单,但证明过程较繁琐,一般做为备选方案。辅助线的构造理论同上。我们只须过已知直线上任意一点做一条与已知平面平行的直线即可。可总结为下图方法一αBAC例 2 如图,在几何体 ABCDE 中,四边形 ABCD 是矩形,AB⊥平面 BEC,BE⊥EC,AB=BE=EC=2,G,F 分别是线段 BE,DC 的中点.求证:GF∥平面 ADE;【答案】解法一:(1)证明:如图,取 AE 的中点 H,连接 HG,HD,又 G 是 BE 的中点,因此 GH∥AB,且 GH=AB.又 F 是 CD 的中点,因此 DF=CD.由四边形 ABCD 是矩形得,AB∥CD,AB=CD,因此 GH∥D...