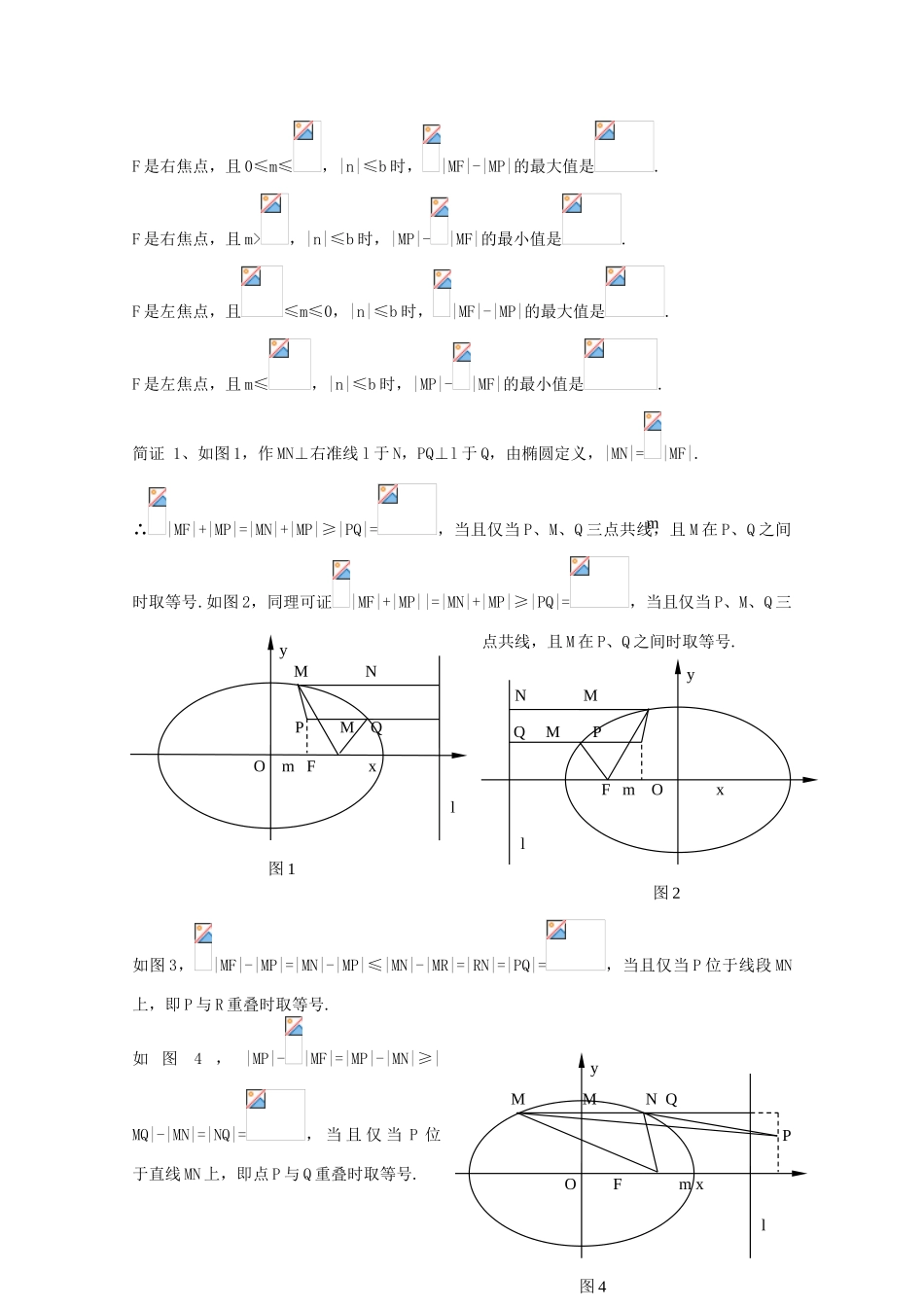
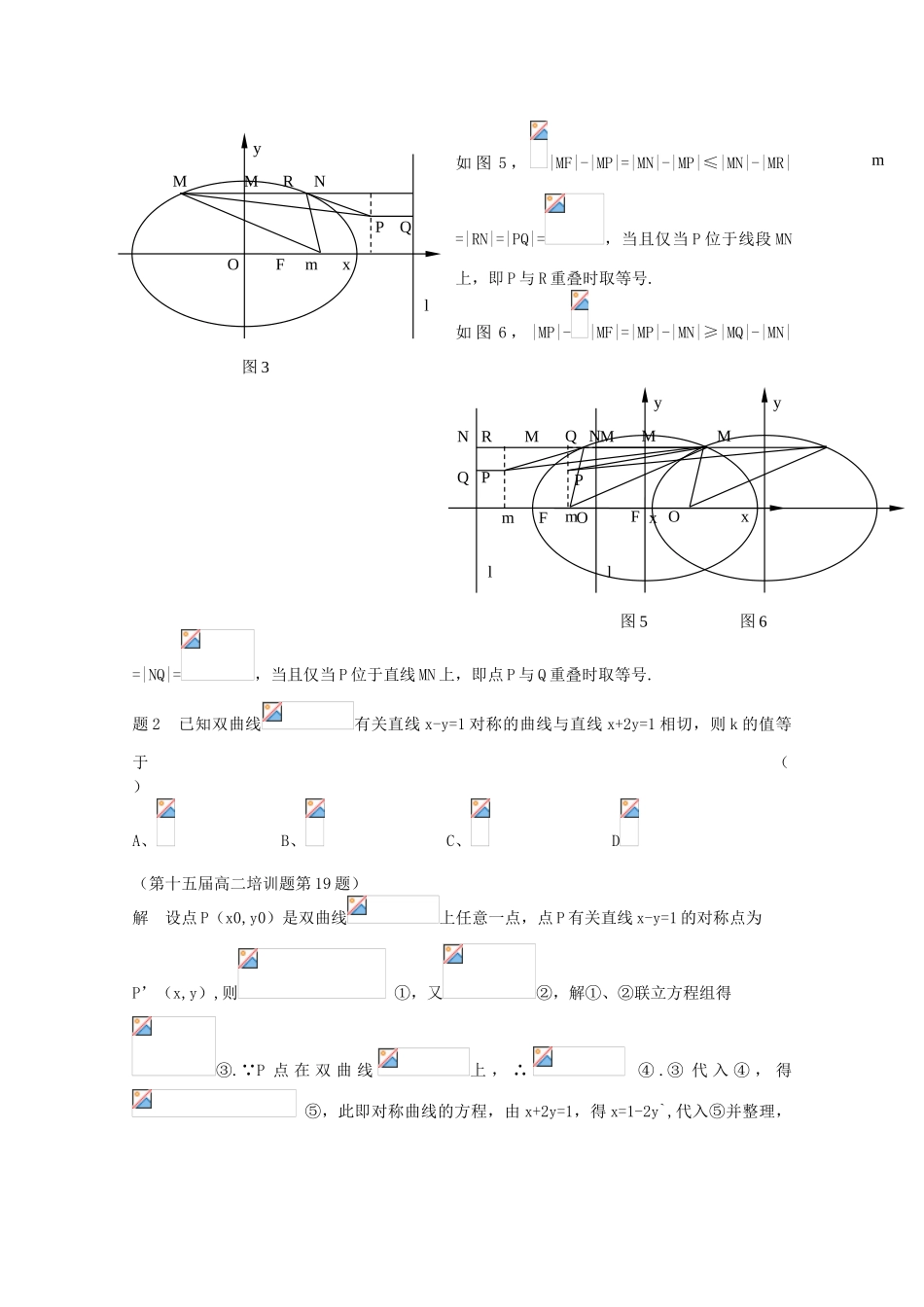
高考理科数学必考点解题措施秘籍:解析几何 3题 1.点,点 F 是椭圆的右焦点,点 P(6,2),那么 3|MF|-|MP|的最大值是 ,此时点 M的坐标是 .解 在 椭 圆中 ,,则,因此椭圆的右焦点 F 的坐标为(1,0),离心率,右准线,显然点 P(6,2)在椭圆的外部.过点 P、M 分别作 PG⊥于 G,MD⊥ 于 D,过点 P 作 PQ⊥MD 于 Q,由椭圆的定义知,3|MF|-|MP|=|MD|-|MP|≤|MD|-|MQ|=|QD|=|PG|=9-6=3,当且仅当点 P 位于线段 MD 上,即点 P 与 Q 点重叠时取等号.由点 P 位于线段 MD 上,MD⊥ 及点 P(6,2),知点 M 的纵坐标为 2,设 M 的横坐标为,即M(,2),则有,解得,因此 3|MF|-|MP|的最大值是 3,此时点M 的坐标是(,2).评析 若设点 M 的坐标为(x,y),则可将 3|MF|-|MP|表达成 x、y 的二元无理函数,然后再求其最大值,可想而知,这是一件相称麻烦的事,运用椭圆的定义,将 3|MF|-|MP|转化为||MD|-|MP|,就把无理运算转化为有理运算,从而大大简化理解题过程.拓展 将此题引伸拓广,可得定理 M 是椭圆 E:上的动点,F 是椭圆 E 的一种焦点,为椭圆 E 的半焦距,P(m,n)为定点.若点 P 在椭圆 E 内,则当 F 是右焦点时,|MF|+|MP|的最小值是;当 F 是左焦点时,|MF|+|MP|的最小值是.若点 P 在椭圆 E 外,则-3 O 1 3 6 9 xM M Q D y P Gl F F 是右焦点,且 0≤m≤,|n|≤b 时,|MF|-|MP|的最大值是.F 是右焦点,且 m>,|n|≤b 时,|MP|-|MF|的最小值是.F 是左焦点,且≤m≤0,|n|≤b 时,|MF|-|MP|的最大值是.F 是左焦点,且 m≤,|n|≤b 时,|MP|-|MF|的最小值是.简证 1、如图 1,作 MN⊥右准线 l 于 N,PQ⊥l 于 Q,由椭圆定义,|MN|=|MF|.∴|MF|+|MP|=|MN|+|MP|≥|PQ|=,当且仅当 P、M、Q 三点共线,且 M 在 P、Q 之间时取等号.如图 2,同理可证|MF|+|MP||=|MN|+|MP|≥|PQ|=,当且仅当 P、M、Q 三点共线,且 M 在 P、Q 之间时取等号.如图 3,|MF|-|MP|=|MN|-|MP|≤|MN|-|MR|=|RN|=|PQ|=,当且仅当 P 位于线段 MN上,即 P 与 R 重叠时取等号.如 图4 , |MP|-|MF|=|MP|-|MN|≥|MQ|-|MN|=|NQ|=, 当 且 仅 当 P 位于直线 MN 上,即点 P 与 Q 重叠时取等号.mO m F xM N y P M Ql 图 1 F m O xN M y Q M Pl 图 2 O F m xM M N Qy P l 图 4 如 图 5 ,|MF|-|...