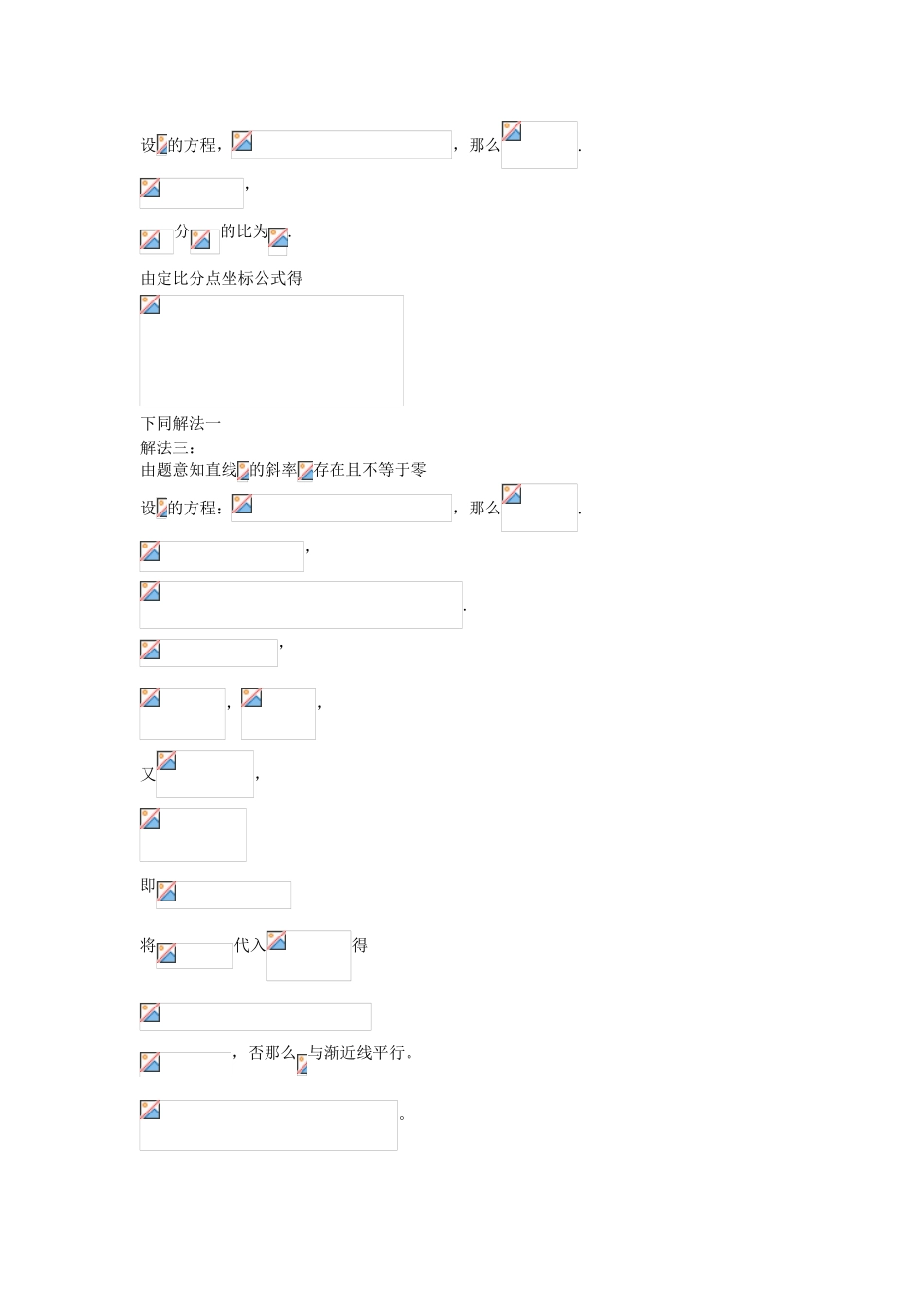
《五年高考真题五星汇编·数学》:第十五章圆锥曲线与方程双曲线 080623doc 高中数学一、考题选析:例 1、(08 上海春) 是双曲线右支上的一点,双曲线的一条渐近线方程为。设分不为双曲线的左、右焦点. 假设,那么 ;例 2、(07 海南) 双曲线的顶点到渐近线的距离为 2,焦点到渐近线的距离为 6,那么该双曲线的离心率为 ;例 3、(07 辽宁) 设为双曲线上的一点,是该双曲线的两个焦点,假设,那么的面积为〔 〕A、B、C、D、例 4、(05 全国Ⅲ) 双曲线的焦点为,点在双曲线上且,那么点到轴的距离为〔 〕A 、 B 、 C、 D、例 5、(06 山东 21) 双曲线与椭圆有相似的热点,直线=为 C 的一条渐近线。〔1〕求双曲线 C 的方程;〔2〕过点(0,4)的直线 l,求双曲线于两点,交轴于点〔点与的顶点不重叠〕。当 =,且时,求点的坐标。解:〔Ⅰ〕设双曲线方程为, 由椭圆 求得两焦点为,有关双曲线,又为双曲线的一条渐近线 解得 ,双曲线的方程为〔Ⅱ〕解法一:由题意知直线 的斜率存在且不等于零。设 的方程:,那么在双曲线上,同理有:假设那么直线 过顶点,不合题意.是二次方程的两根.,目前.所求的坐标为.解法二:由题意知直线 的斜率存在且不等于零设 的方程,,那么.,分的比为.由定比分点坐标公式得下同解法一解法三:由题意知直线 的斜率存在且不等于零设 的方程:,那么.,.,,,又,即将代入得,否那么 与渐近线平行。。解法四:由题意知直线 l 得斜率 k 存在且不等于零,设 的方程:,那么,。同理.即。〔*〕又消去 y 得.当时,那么直线 l 与双曲线得渐近线平行,不合题意,。由韦达定理有:代入〔*〕式得所求 Q 点的坐标为。例 6、〔04 广东 20〕某中心接到其正东、正西、正北方向三个观测点的汇报:正西、正北两个观测点同步听到了一声巨响,正东观测点听到的时刻比其他两观测点晚 4s. 各观测点到该中心的距离差不多上 1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :有关各点均在同一平面上)。解:如图,以接报中心为原点 O,正东、正北方向为 x 轴、y 轴正向,建立直角坐标系.设A、B、C分不是西、东、北观测点,那么A〔-1020,0〕,B〔1020,0〕,C〔0,1020〕设 P〔x,y〕为巨响为生点,由 A、C 同步听到巨响声,得|PA|=|PB|,故 P 在 AC 的垂直平分线 PO 上 , PO 的 方 程 为 y= - x , 因 B 点 比 A 点 晚 4s 听 ...