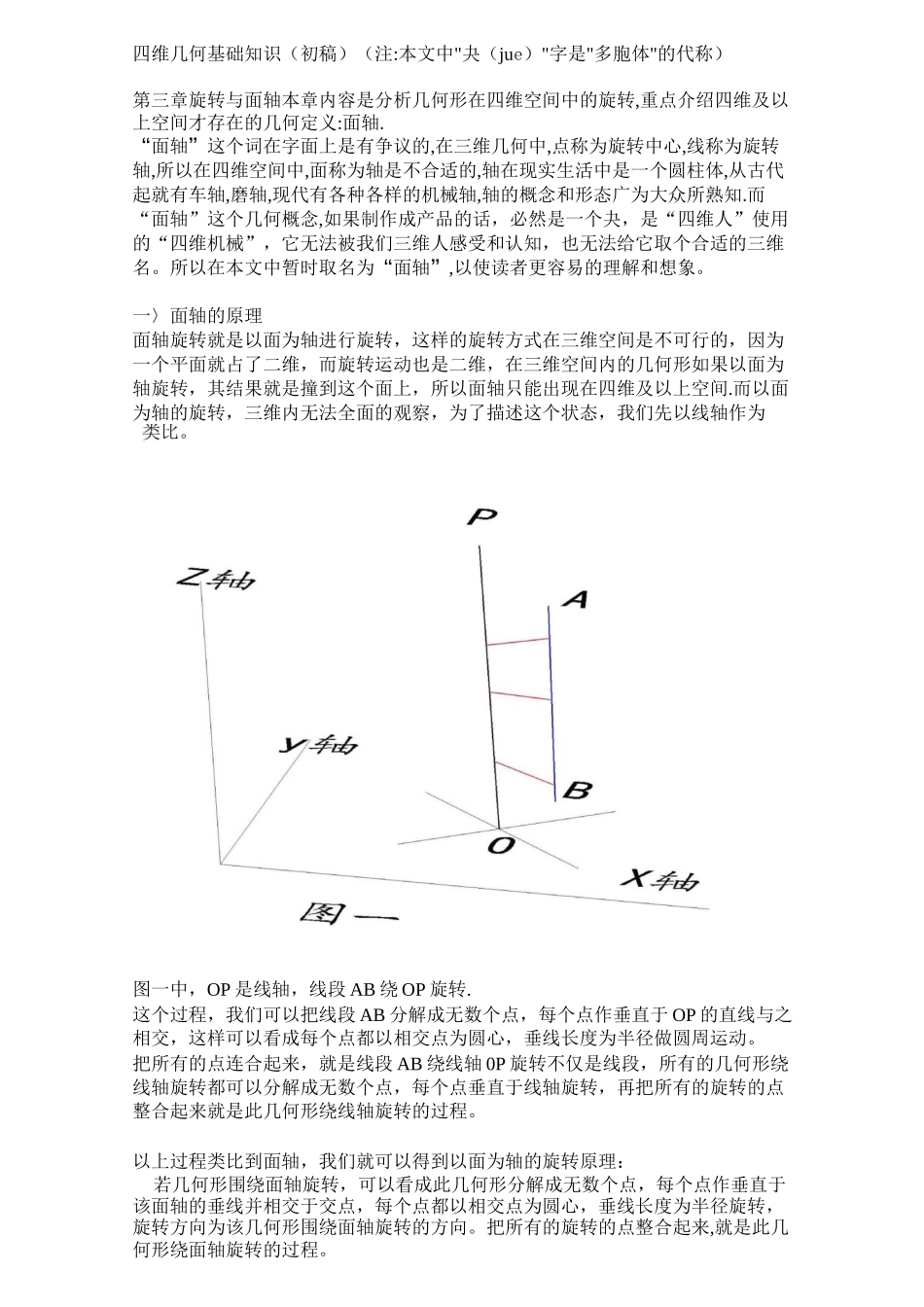
四维几何基础知识(初稿)(注:本文中"夬(jue)"字是"多胞体"的代称)第三章旋转与面轴本章内容是分析几何形在四维空间中的旋转,重点介绍四维及以上空间才存在的几何定义:面轴.“面轴”这个词在字面上是有争议的,在三维几何中,点称为旋转中心,线称为旋转轴,所以在四维空间中,面称为轴是不合适的,轴在现实生活中是一个圆柱体,从古代起就有车轴,磨轴,现代有各种各样的机械轴,轴的概念和形态广为大众所熟知.而“面轴”这个几何概念,如果制作成产品的话,必然是一个夬,是“四维人”使用的“四维机械”,它无法被我们三维人感受和认知,也无法给它取个合适的三维名。所以在本文中暂时取名为“面轴”,以使读者更容易的理解和想象。一〉面轴的原理面轴旋转就是以面为轴进行旋转,这样的旋转方式在三维空间是不可行的,因为一个平面就占了二维,而旋转运动也是二维,在三维空间内的几何形如果以面为轴旋转,其结果就是撞到这个面上,所以面轴只能出现在四维及以上空间.而以面为轴的旋转,三维内无法全面的观察,为了描述这个状态,我们先以线轴作为图一中,OP 是线轴,线段 AB 绕 OP 旋转.这个过程,我们可以把线段 AB 分解成无数个点,每个点作垂直于 OP 的直线与之相交,这样可以看成每个点都以相交点为圆心,垂线长度为半径做圆周运动。把所有的点连合起来,就是线段 AB 绕线轴 0P 旋转不仅是线段,所有的几何形绕线轴旋转都可以分解成无数个点,每个点垂直于线轴旋转,再把所有的旋转的点整合起来就是此几何形绕线轴旋转的过程。以上过程类比到面轴,我们就可以得到以面为轴的旋转原理:若几何形围绕面轴旋转,可以看成此几何形分解成无数个点,每个点作垂直于该面轴的垂线并相交于交点,每个点都以相交点为圆心,垂线长度为半径旋转,旋转方向为该几何形围绕面轴旋转的方向。把所有的旋转的点整合起来,就是此几何形绕面轴旋转的过程。这个过程描述比较复杂,但有另外一个描述比较简单,那就是“镜子原理”,把面轴看作是一面镜子,当几何形绕面轴旋转 180 度后,它的位置和形态就是“镜子中的自己“二>旋转方向.因为面轴本身是二维的,所以旋转的方向是 360 度,这点与一维线轴有区别.当我们确定面轴时,还要说明旋转的方向,这样才能保证旋转轨迹的唯一性.三>定位线和定位面在四维空间中,还有以中心点,以线为轴的旋转,这样的旋转最终都要转化为以面为轴的旋转,也需要说明旋转的方向,要实现这一点,就要引入定位线和定位面的概念.我们...