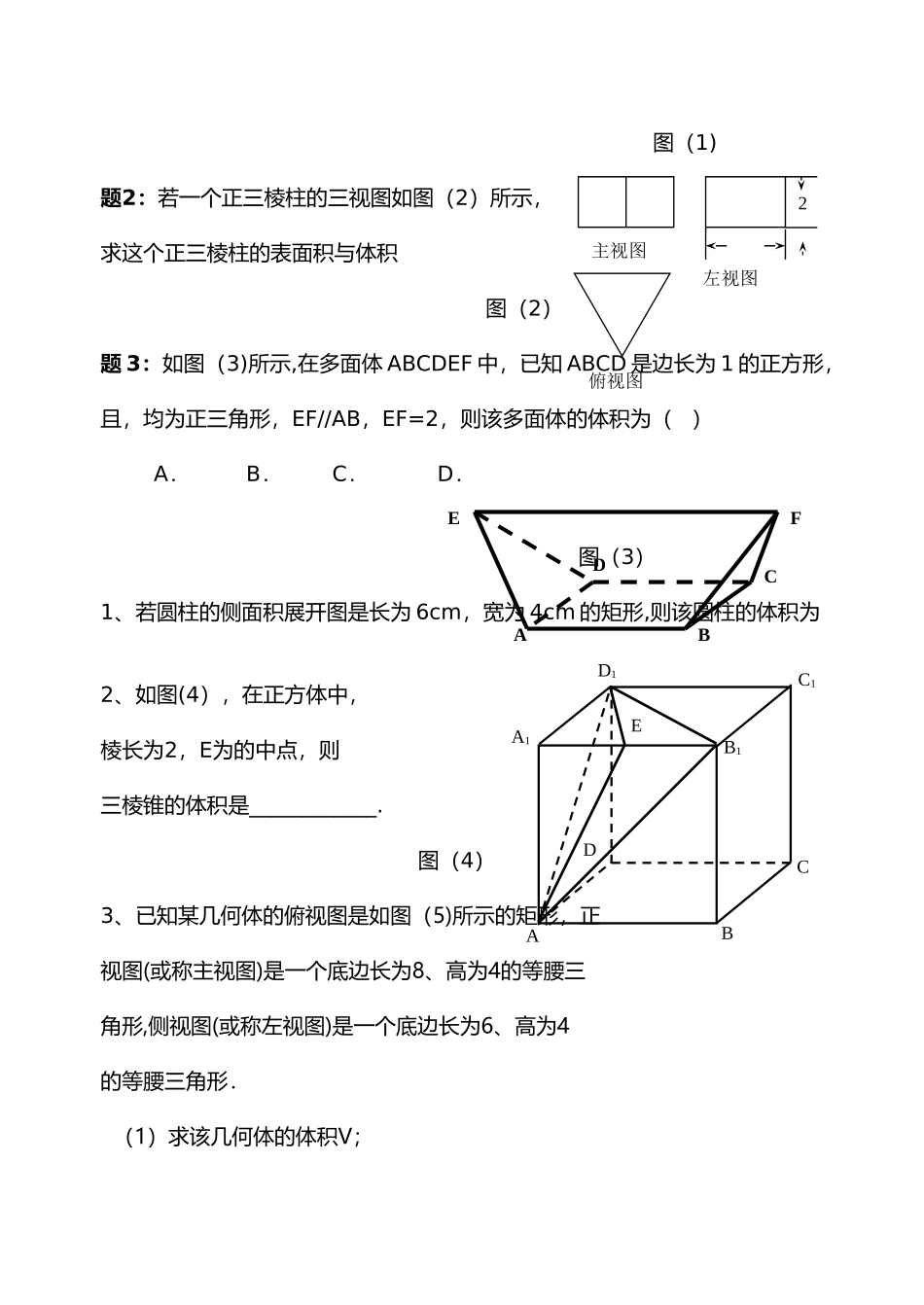
一、知识回顾(1)棱柱、棱锥、棱台的表面积 = 侧面积 + ______________;(2)圆柱:r 为底面半径,l 为母线长侧面积为_______________;表面积为_______________.圆锥:r 为底面半径,l 为母线长侧面积为_______________;表面积为_______________.圆台:r’、r 分别为上、下底面半径,l 为母线长侧面积为_______________;表面积为_______________.(3)柱体体积公式:________________________;(S 为底面积,h 为高)锥体体积公式:________________________;(S 为底面积,h 为高)台体体积公式:________________________;(S’、S 分别为上、下底面面积,h 为高)二、例题讲解题 1:如图(1)所示,直角梯形 ABCD 绕着它的底边 AB 所在的直线旋转一周所得的几何体的表面积是______________;体积是______________。483ADCB图(1)题2:若一个正三棱柱的三视图如图(2)所示,求这个正三棱柱的表面积与体积 图(2)题 3:如图(3)所示,在多面体 ABCDEF 中,已知 ABCD 是边长为 1 的正方形,且,均为正三角形,EF//AB,EF=2,则该多面体的体积为( )A. B. C. D.图(3)1、若圆柱的侧面积展开图是长为 6cm,宽为 4cm 的矩形,则该圆柱的体积为2、如图(4),在正方体中,棱长为2,E为的中点,则三棱锥的体积是____________. 图(4)3、已知某几何体的俯视图是如图(5)所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形. (1)求该几何体的体积V;EABDCF左视图俯视图主视图2CBADC1B1EA1D1 (2)求该几何体的侧面积 S。图(5)(选做题)4、如图(6),一个圆锥的底面半径为 2cm,高为 6cm,在其中有一个高为 xcm 的内接圆柱。(1)试用 x 表示圆柱的侧面积;(2)当 x 为何值时,圆柱的侧面积最大?一、选择题(每小题 5 分,共计 60 分。请把选择答案填在答题卡上。)1.以三棱锥各面重心为顶点,得到一个新三棱锥,它的表面积是原三棱锥表面积的A. B。 C。 D。2.正六棱锥底面边长为 a,体积为,则侧棱与底面所成的角等于A. B。 C. D。3.有棱长为 6 的正四面体 S—ABC,分别在棱 SA,SB,SC 上,且 S=2,S=3,S=4,则截面将此正四面体分成的两部分体积之比为 A. B。 C。 D.4。长方体的全面积是 11,十二条棱长的和是 24,则它的一条对角线长是A.. B。 C. 5 D。6 5。圆锥的全面积是侧面积的 2 倍...