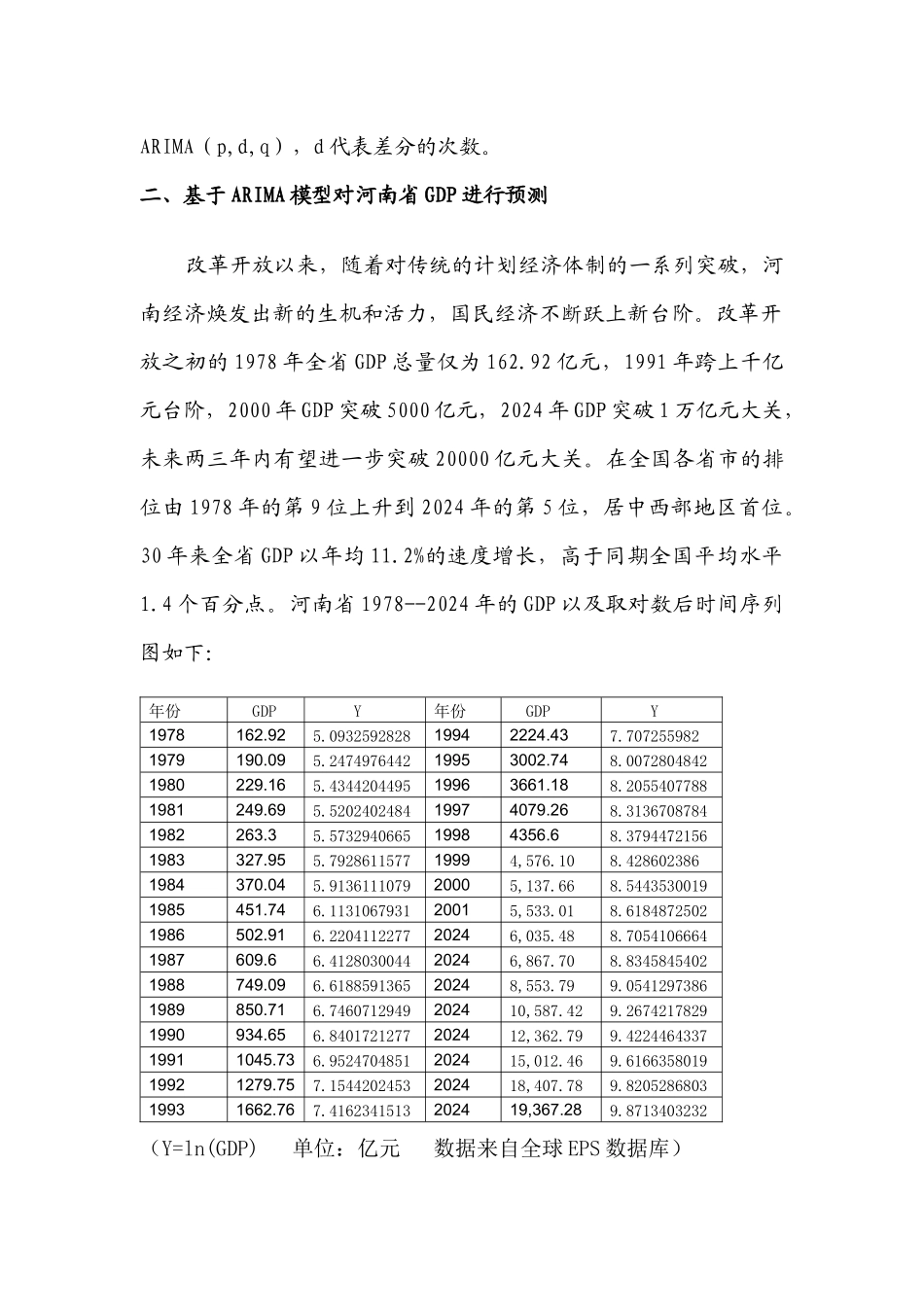
基于 ARIMA 模型对河南省 2024 年 GDP 预测摘要:ARIMA 模型是对 ARMA 模型的差分得到的平稳时间序列模型,具有序列相关性,本文收集了 1978-2024 年河南省 GDP 数据,根据ARIMA 模型的性质、利用统计软件对河南省 2024 年 GDP 进行预测。关键字:平稳性、ARMA 模型、ARIMA 模型 由于 2024 年金融海啸的全面性的爆发,我国的整体经济水平难免呈现不良的进展趋势,4 万亿的救市计划,终于达到 2024 年的保八目标。在这个时候假如对我国 GDP 进行预测,难免有些偏差,因此本文选择受金融危机影响较小、地处中原、经济持续平稳增长的河南省为例,收集改革开放 30 年来的数据对 2024 年的 GDP 进行预测。GDP 时间序列具有明显的增长趋势,因此 ARMA 模型显然的不稳定的,基于 ARMA 模型进行差分,发现二次差分的结果不仅稳定,而且表示出良好的序列相关性,所以能用 ARMIMA 模型对为例 GDP 进行预测。比较原始值 GDP 和预测值 GDPF,两曲线吻合的比较好。一、ARIMA 模型的建立时间序列模型有四种:自回归模型 AR、移动平均模型 MA、自回归移动平均模型 ARMA、自回归差分移动平均模型 ARIMA,可以说前三种都是 ARIMA 模型的特别形式。1. 自回归模型 AR(p) p 阶自回归模型记作 AR(p),满足下面的方程: 其中:参数 c 为常数;1,2 ,…,p 是自回归模型系数;p 为自回归模型阶数;是均值为 0 方差为 的白噪声序列。 2. 移动平均模型 MA(q) q 阶移动平均模型记作 MA(q) ,满足下面的方程: 其中:参数为常数;是 q 阶移动平均模型的系数;是均值为 0,方差为 的白噪声序列。 3. ARMA(p,q)模型 显然此模型是模型 AR(p)与 MA(q)的组合形式,称为混合模型,常记作 ARMA(p,q)。当 p=0 时,ARMA(0, q) = MA(q);当 q = 0 时,ARMA(p, 0) = AR(p)。4. ARIMA(p,d,q)模型 对于非平稳序列,经过几次差分后,假如能得到平稳的时间序列,就称这样的序列为单整序列。设是 d 阶单整序列,记作:~ I(d),则 为平稳序列,即~ I(0) ,于是可以对 建立 ARMA(p,q) 模型 : 假如时间序列经过 d 次差分后是一个 ARIMA(p,q)过程,则称原时间序列是一个 p 阶自回归、d 阶求整、q 阶移动平均过程,记作ARIMA(p,d,q),d 代表差分的次数。二、基于 ARIMA 模型对河南省 GDP 进行预测 改革开放以来,随着对传统的计划经济体制的一系列突破,河南经...